Условие задачи:
На одном из концов однородного стержня прикреплен груз массой 3 кг. Если стержень на расстоянии 1/5 его длины от груза подпереть, то он окажется в равновесии. Чему равна масса стержня?
Задача №3.1.15 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(M=3\) кг, \(l=\frac{L}{5}\), \(m-?\)
Решение задачи:
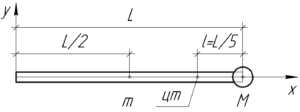Изобразим схему для решения этой задачи и введем координатные оси, как показано на ней. Так как схема симметрична относительно оси \(x\), то одна из координат центра тяжести всей системы \(y_{цт}\) равна нулю.
Если стержень подпереть в некоторой точке и после этого он окажется в равновесии, значит в этой точке находится центр тяжести системы. Поэтому:
\[{x_{цт}} = L – l = L – \frac{L}{5}\]
\[{x_{цт}} = \frac{{4L}}{5}\;\;\;\;(1)\]
С другой стороны эту же координату центра тяжести можно найти по следующей формуле:
\[{x_{цт}} = \frac{{\sum\limits_{i = 1}^n {{m_i}g{x_i}} }}{{\sum\limits_{i = 1}^n {{m_i}g} }}\]
Здесь \(m_i\) – это масса i-того тела, а \(x_i\) – координата центра масс i-того тела. Применительно к этой задаче имеем:
\[{x_{цт}} = \frac{{m \cdot g \cdot 0,5L + M \cdot g \cdot L}}{{m \cdot g + M \cdot g}}\]
\[{x_{цт}} = \frac{{\left( {m + 2M} \right)L}}{{2\left( {m + M} \right)}}\;\;\;\;(2)\]
Приравняем правые части равенств (1) и (2):
\[\frac{{\left( {m + 2M} \right)L}}{{2\left( {m + M} \right)}} = \frac{{4L}}{5}\]
\[\frac{{m + 2M}}{{2\left( {m + M} \right)}} = \frac{4}{5}\]
Перемножим “крест – накрест”:
\[5m + 10M = 8m + 8M\]
\[2M = 3m\]
\[m = \frac{{2M}}{3}\]
Численно масса стержня равна:
\[m = \frac{{2 \cdot 3}}{3} = 2\;кг\]
Ответ: 2 кг.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.1.14 Три однородных шара массой 1, 2 и 2 кг укреплены на легко стержне. Центр 2-ого шара
3.1.16 Однородная доска массой 10 кг подперта на расстоянии 0,25 её длины от конца. Какую
3.1.17 Рабочий удерживает за один конец доску массой 50 кг. С горизонтальной поверхностью
Через правило моментов можно решить задачу более короче)
Если взять точку, относительно которой будем рассматривать моменты сил, те в точке приложения опоры. Очень простое уравнение получается.
Согласен, у вас решение займет 3 строки. Вы записываете правило моментов относительно точки опоры, получаете
\[\begin{gathered}
M \cdot \frac{L}{5} = m \cdot \left( {\frac{L}{2} – \frac{L}{5}} \right) \hfill \\
M \cdot \frac{L}{5} = m \cdot \frac{{3L}}{{10}} \hfill \\
m = \frac{{2M}}{3} \hfill \\
\end{gathered} \]
Ваше решение гораздо короче)