Решение: При фотографировании предмета с расстояния 1 м высота изображения равна 6 см

Условие задачи:

При фотографировании предмета с расстояния 1 м высота изображения равна 6 см, а при фотографировании с расстояния 5 м высота изображения равна 1 см. Определить фокусное расстояние объектива фотоаппарата.

Задача №10.5.69 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(d_1=1\) м, \(h_1=6\) см, \(d_2=5\) м, \(h_2=1\) см, \(F-?\)

Решение задачи:

В фотоаппарате установлена собирающая линза, поскольку только она может давать действительное изображение. При этом, очевидно, что предмет всегда расположен левее относительно переднего фокуса линзы (\({d} > {F}\)).

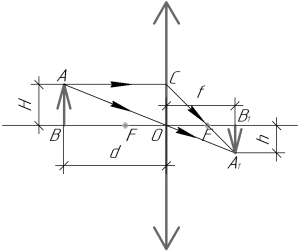
Покажем общий принцип построения изображения в собирающей линзе для случая \({d} > {F}\) (см. рисунок). Чтобы построить изображение точки A в собирающей линзе, нужно провести через точку A два луча: один параллельно главной оптической оси, а второй через главный оптический центр O. Первый луч, преломившись в линзе, пройдет через задний фокус линзы. Второй луч проходит через линзу, не преломляясь. На пересечении этих лучей и будет находиться точка A₁. Проекция этой точки на главную оптическую ось есть точка B₁. Вот и все, изображение телебашни построено. Как мы видим, оно получилось действительным (поскольку получается на сходящемся пучке лучей), перевернутым и (скорее всего) уменьшенным.

Запишем формулу тонкой линзы:

\[\frac{1}{F} = \frac{1}{d} + \frac{1}{f}\;\;\;\;(1)\]

В этой формуле \(F\) — фокусное расстояние линзы, знак перед ним «+», поскольку линза — собирающая, \(d\) — расстояние от линзы до предмета, знак перед ним «+», поскольку предмет — действительный (в случае одиночной линзы предмет всегда действительный, оно бывает мнимым в случае системы линз), \(f\) — расстояние от линзы до изображения, знак перед ним «+», поскольку изображение — действительное (то есть образуется на сходящемся пучке лучей — смотрите рисунок).

Из подобия треугольников AOB и A₁OB₁ по трем углам следует, что (при этом эти две дроби ещё равны и поперечному увеличению (хотя в этом случае корректнее назвать уменьшением) линзы \(\Gamma\)):

\[\Gamma = \frac{f}{d} = \frac{h}{H}\;\;\;\;(2)\]

Тогда из формулы (1) выразим неизвестное расстояние от линзы до изображения \(f\):

\[\frac{1}{f} = \frac{1}{F} — \frac{1}{d}\]

\[\frac{1}{f} = \frac{{d — F}}{{dF}}\]

\[f = \frac{{dF}}{{d — F}}\;\;\;\;(3)\]

Подставим выражение (3) в формулу (2):

\[\frac{{dF}}{{d\left( {d — F} \right)}} = \frac{h}{H}\]

\[\frac{F}{{d — F}} = \frac{h}{H}\]

Полученную формулу запишем для двух случаев, рассматриваемых в этой задаче:

\[\left\{ \begin{gathered}
\frac{F}{{{d_1} — F}} = \frac{{{h_1}}}{H} \hfill \\
\frac{F}{{{d_2} — F}} = \frac{{{h_2}}}{H} \hfill \\
\end{gathered} \right.\]

Поделим верхнее уравнение на нижнее:

\[\frac{{{d_2} — F}}{{{d_1} — F}} = \frac{{{h_1}}}{{{h_2}}}\]

Перемножим «крест-накрест», чтобы решить это уравнение:

\[\left( {{d_2} — F} \right){h_2} = \left( {{d_1} — F} \right){h_1}\]

Раскроем скобки в обеих частях уравнения:

\[{d_2}{h_2} — F{h_2} = {d_1}{h_1} — F{h_1}\]

Все члены с искомым фокусным расстоянием \(F\) перенесем в левую сторону, остальные — в правую:

\[F{h_1} — F{h_2} = {d_1}{h_1} — {d_2}{h_2}\]

\[F\left( {{h_1} — {h_2}} \right) = {d_1}{h_1} — {d_2}{h_2}\]

Окончательно получим такое решение представленной задачи в общем виде:

\[F = \frac{{{d_1}{h_1} — {d_2}{h_2}}}{{{h_1} — {h_2}}}\]

Если подставить в эту формулу значения величин из условия задачи, то мы получим ответ (не забываем переводить эти значения в систему СИ):