Условие задачи:

Два сосуда объемом 2 и 4 л, заполненные одинаковым газом, соединены трубкой с краном. При закрытом кране давление газа в первом сосуде 400 кПа, а во втором — 200 кПа. На сколько изменится масса газа в первом сосуде после открытия крана, если первоначально она была 18 г и процесс изотермический?

Задача №4.3.27 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$V_1=2$ л, $V_2=4$ л, $p_1=400$ кПа, $p_2=200$ кПа, $m_1=18$ г, $\Delta m-?$

Решение задачи:

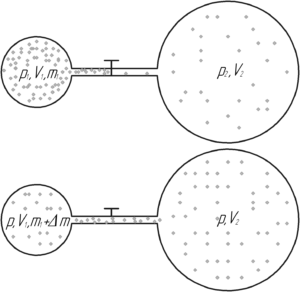После открытия крана газа из первого сосуда перетечет во второй сосуд, при этом давление в сосудах станет одинаковым и равным $p_0$.

Для решения задачи запишем 4 раза уравнение Клапейрона-Менделеева: вначале (до открытия крана) для газа в первом (левом) и втором (правом) сосуде, для части газа в первом сосуде и для всего газа в конце (после открытия крана):

$$\left\{ \begin{gathered} {p_1}{V_1} = \frac{{{m_1}}}{M}RT\;\;\;\;(1) \hfill \\ {p_2}{V_2} = \frac{{{m_2}}}{M}RT\;\;\;\;(2) \hfill \\ p{V_1} = \frac{{{m_1} + \Delta m}}{M}RT\;\;\;\;(3) \hfill \\ p\left( {{V_1} + {V_2}} \right) = \frac{{{m_1} + {m_2}}}{M}RT\;\;\;\;(4) \hfill \\ \end{gathered} \right.$$

Сложив уравнения (1) и (2) и сравнив правую часть этой суммы с правой частью уравнения (4), можно увидеть, что они равны:

$$\left\{ \begin{gathered} {p_1}{V_1} + {p_2}{V_2} = \frac{{{m_1} + {m_2}}}{M}RT \hfill \\ p\left( {{V_1} + {V_2}} \right) = \frac{{{m_1} + {m_2}}}{M}RT \hfill \\ \end{gathered} \right.$$

Тогда видно, что:

$${p_1}{V_1} + {p_2}{V_2} = p\left( {{V_1} + {V_2}} \right) \Rightarrow p = \frac{{{p_1}{V_1} + {p_2}{V_2}}}{{{V_1} + {V_2}}}$$

Теперь поделим уравнение (3) на уравнение (1) и получим:

$$\frac{p}{{{p_1}}} = \frac{{{m_1} + \Delta m}}{{{m_1}}}$$

Подставим теперь в эту формулу полученное нами выражение для $p$ и выразим искомое $\Delta m$:

$$\frac{{{p_1}{V_1} + {p_2}{V_2}}}{{{p_1}\left( {{V_1} + {V_2}} \right)}} = \frac{{{m_1} + \Delta m}}{{{m_1}}}$$

Формула для нахождения ответа в общем виде выглядит следующим образом:

$$\Delta m = {m_1}\left( {\frac{{{p_1}{V_1} + {p_2}V}}{{{p_1}\left( {{V_1} + {V_2}} \right)}} — 1} \right)$$

Подставим исходные величины в системе СИ и будет иметь численный ответ:

$$\Delta m = 0,018\left( {\frac{{400 \cdot {{10}^3} \cdot 0,002 + 200 \cdot {{10}^3} \cdot 0,004}}{{400 \cdot {{10}^3}\left( {0,002 + 0,004} \right)}} — 1} \right) =  — 0,006\; кг = — 6\; г$$

Знак «минус» показывает, что масса газа в первом сосуде уменьшится.

Ответ: 6 г.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

4.3.26 В цилиндре под поршнем находится газ. Масса поршня 0,6 кг
4.3.28 В цилиндре под поршнем находится воздух. Вес поршня 60 Н
4.3.29 В цилиндре под поршнем находится вода массой 35 мг и пар массой 25 мг