Условие задачи:

Бутылка с газом закрыта пробкой, площадь сечения которой 2,5 см². До какой температуры надо нагреть газ, чтобы пробка вылетела из бутылки, если удерживающая ее сила 12 Н? Давление воздуха в бутылке равно атмосферному, а температура -3° C.

Задача №4.3.25 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(S=2,5\) см², \(F=12\) Н, \(p_0=10^5\) Па, \(t_0=-3^\circ\) C, \(T_1-?\)

Решение задачи:

Важный момент в таких задачах: не нужно забывать, что на пробку действует внешнее атмосферное давление!

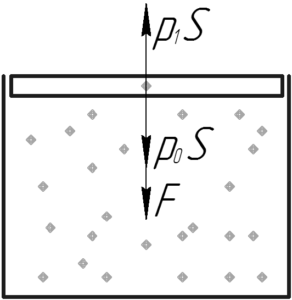
До момента вылета пробки из бутылки процесс нагревания газа является изохорным, поэтому запишем закон Шарля и условие равновесия пробки (1-й закон Ньютона) непосредственно перед ее вылетом (смотри рисунок).

\[\frac{{{p_0}}}{{{T_0}}} = \frac{{{p_1}}}{{{T_1}}}\;\;\;\;(1)\]

\[{p_1}S = {p_0}S + F\;\;\;\;(2)\]

Из закона Шарля (1) выразим \(p_1\) и подставим в первый закон Ньютона (2):

\[{p_1} = \frac{{{p_0}{T_1}}}{{{T_0}}}\]

\[\left( {{p_1} — {p_0}} \right)S = F\]

\[\left( {\frac{{{p_0}{T_1}}}{{{T_0}}} — {p_0}} \right)S = F\]

\[{p_0}\left( {\frac{{{T_1}}}{{{T_0}}} — 1} \right)S = F\]

Осталось выразить искомую температуру \(T_1\):

\[\frac{{{T_1}}}{{{T_0}}} — 1 = \frac{F}{{{p_0}S}}\]

\[\frac{{{T_1}}}{{{T_0}}} = \frac{F}{{{p_0}S}} + 1\]

\[{T_1} = {T_0}\left( {\frac{F}{{{p_0}S}} + 1} \right)\]

Так как начальная формула дана в градусах Цельсия, то конечная формула будет иметь вид:

\[{T_1} = \left( {{t_0} + 273} \right)\left( {\frac{F}{{{p_0}S}} + 1} \right)\]

Подставим исходные данные в системе измерения СИ. Получим численный ответ:

\[{T_1} = \left( { — 3 + 273} \right)\left( {\frac{{12}}{{{{10}^5} \cdot 2,5 \cdot {{10}^{ — 4}}}} + 1} \right) = 399,6\; К \approx 400\; К\]

Ответ: 400 К.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

4.3.24 Давление азота в электрической лампочке объемом 0,15 л равно 68 кПа
4.3.26 В цилиндре под поршнем находится газ. Масса поршня 0,6 кг
4.3.27 Два сосуда объемом 2 и 4 л, заполненные одинаковым газом, соединены