Условие задачи:

На экваторе некоторой планеты тела весят втрое меньше, чем на полюсе. Период обращения этой планеты вокруг своей оси равен 2 ч. Определить среднюю плотность планеты.

Задача №2.5.17 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(P_э=\frac{1}{3}P_п\), \(T=2\) ч, \(\rho-?\)

Решение задачи:

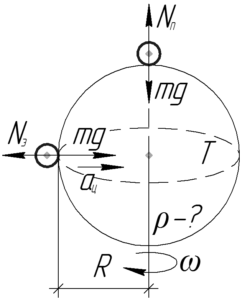Тело на экваторе вращается вместе с планетой по окружности радиуса \(R\) (радиус планеты). Применив второй закон Ньютона, получим следующее равенство:

\[mg — {N_э} = m{a_ц}\;\;\;\;(1)\]

Тело на полюсе лежит на оси вращения планеты, поэтому оно вращается лишь вокруг себя. Запишем первый закон Ньютона:

\[mg = {N_п}\;\;\;\;(2)\]

По третьему закону Ньютона сила реакции опоры (\(N_э\) и \(N_п\)) равна весу тела (\(P_э\) и \(P_п\) соответственно). Учтите, что эти силы хоть и равны по величине, но противоположны по направлению и приложены к разным телам. С учетом этого запишем равенства (1) и (2) в такой системе:

\[\left\{ \begin{gathered}
{P_э} = mg — m{a_ц} \hfill \\
{P_п} = mg \hfill \\
\end{gathered} \right.\]

Поделим нижнее равенство на верхнее. Так как \(P_э=\frac{1}{3}P_п\), то получим:

\[\frac{g}{{g — {a_ц}}} = 3\]

\[3g — 3{a_ц} = g\]

\[2g = 3{a_ц}\;\;\;\;(3)\]

Поскольку в задаче нужно узнать среднюю плотность планеты \(\rho\), то запишем такие формулы: во-первых, формулу определения ускорения свободного падения \(g\) на поверхности планеты, во-вторых, формулу определения массы через плотность и объем, в-третьих, формулу определения объема шара.

\[g = G\frac{M}{{{R^2}}}\;\;\;\;(4)\]

\[M = \rho  \cdot V\;\;\;\;(5)\]

\[V = \frac{4}{3}\pi {R^3}\;\;\;\;(6)\]

Подставив (6) в (5), а полученное в (4), получим:

\[g = \frac{4}{3}\pi G\rho R\;\;\;\;(7)\]

Чтобы выразить центростремительное ускорение \(a_ц\) через период вращения планеты \(T\) запишем такие формулы: формулу определения ускорения \(a_ц\) через угловую скорость \(\omega\) и формулу связи последней с периодом вращения \(T\).

\[{a_ц} = {\omega ^2}R\]

\[\omega  = \frac{{2\pi }}{T}\]

В итоге:

\[{a_ц} = \frac{{4{\pi ^2}}}{{{T^2}}}R\;\;\;\;(8)\]

Подставим выражения (7) и (8) в ранее полученное равенство (3):

\[\frac{8}{3}\pi G\rho R = \frac{{12{\pi ^2}}}{{{T^2}}}R\]

\[\rho  = \frac{{9\pi }}{{2G{T^2}}}\]

Переведем данный в условии период вращения \(T\) в систему СИ (в секунды):

\[T = 2\;ч = 2 \cdot 3600 = 7200\; с\]

Посчитаем ответ:

\[\rho  = \frac{{9 \cdot 3,14}}{{2 \cdot 6,67 \cdot {{10}^{ — 11}} \cdot {{7200}^2}}} = 4086,5\; кг/м^3 \approx 4\; г/см^3\]

Ответ: 4 г/см³.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.5.16 На экваторе некоторой планеты тела весят вдвое меньше, чем на полюсе. Плотность
2.5.18 Тело поднялось на высоту 1600 км над поверхностью Земли. На сколько процентов
2.5.19 Определить минимальный период обращения спутника нейтронной звезды. Её плотность