Условие задачи:

На экваторе некоторой планеты тела весят вдвое меньше, чем на полюсе. Плотность вещества планеты 3000 кг/м³. Определить период обращения планеты около собственной оси.

Задача №2.5.16 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(P_э=\frac{1}{2}P_п\), \(\rho=3000\) кг/м³, \(T-?\)

Решение задачи:

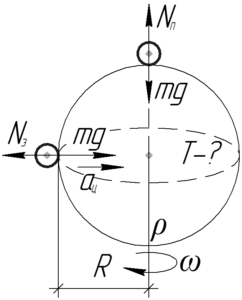Тело на экваторе вращается вместе с планетой по окружности радиуса \(R\), поэтому второй закон Ньютона будет записан в следующем виде:

\[mg — {N_э} = m{a_ц}\]

Тело на полюсе вращается вокруг себя, так как ось вращения планеты проходит через его центр масс. Первый закон Ньютона для этого тела выглядит так:

\[mg = {N_п}\]

Сила реакции опоры равна весу тела по третьему закону Ньютона. Значит \(N_э=P_э\) и \(N_п=P_п\). Записав в другом виде полученные ранее равенства, получим такую систему:

\[\left\{ \begin{gathered}
{P_э} = mg — m{a_ц} \hfill \\
{P_п} = mg \hfill \\
\end{gathered} \right.\]

Поделим первое равенство на второе. Учитывая, что по условию \(P_э=\frac{1}{2}P_п\), имеем:

\[\frac{{g — {a_ц}}}{g} = \frac{1}{2}\]

\[2g — 2{a_ц} = g\]

\[g = 2{a_ц}\;\;\;\;(1)\]

Ускорение свободного падения \(g\) на поверхности планеты можно найти по формуле:

\[g = G\frac{M}{{{R^2}}}\]

Масса планеты равна произведению её средней плотности на объем:

\[M = \rho  \cdot V\]

Объем сферической планеты определим по известной из математики формуле:

\[V = \frac{4}{3}\pi {R^3}\]

Тогда:

\[M = \frac{4}{3}\pi {R^3}\rho \]

\[g = \frac{4}{3}\pi G\frac{{\rho {R^3}}}{{{R^2}}}\]

\[g = \frac{4}{3}\pi G\rho R\;\;\;\;(2)\]

Центростремительное ускорение \(a_ц\) зависит от угловой скорости \(\omega\) и радиуса \(R\).

\[{a_ц} = {\omega ^2}R\]

Угловая скорость \(\omega\) связана с периодом \(T\) по такой формуле:

\[\omega  = \frac{{2\pi }}{T}\]

Значит:

\[{a_ц} = \frac{{4{\pi ^2}}}{{{T^2}}}R\;\;\;\;(3)\]

Подставим выражения (2) и (3) в полученное ранее равенство (1):

\[\frac{4}{3}\pi G\rho R = \frac{{8{\pi ^2}}}{{{T^2}}}R\]

\[\frac{1}{3}G\rho  = \frac{{2\pi }}{{{T^2}}}\]

\[T = \sqrt {\frac{{6\pi }}{{G\rho }}} \]

Посчитаем ответ:

\[T = \sqrt {\frac{{6 \cdot 3,14}}{{6,67 \cdot {{10}^{ — 11}} \cdot 3000}}}  = 9703\; с = 161,7\; мин\]

Ответ: 161,7 мин.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.5.15 Определить плотность шарообразной планеты, если вес тела на полюсе в 2 раза больше
2.5.17 На экваторе некоторой планеты тела весят втрое меньше, чем на полюсе. Период
2.5.18 Тело поднялось на высоту 1600 км над поверхностью Земли. На сколько процентов