Условие задачи:
Вертикально стоящий шест высотой 1,1 м, освещенный Солнцем, отбрасывает на горизонтальную поверхность земли тень длиной 1,3 м, а длина тени от телеграфного столба на 5,2 м больше. Найти высоту столба.
Задача №10.1.20 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(h=1,1\) м, \(l=1,3\) м, \(\Delta l=5,2\) м, \(H-?\)
Решение задачи:
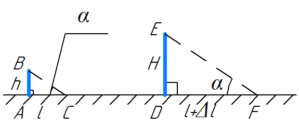 Сделаем рисунок к задаче, на котором изобразим условно вертикально установленные шест и телеграфный столб (на рисунке AB и DE соответственно). Так как угол падения солнечных лучей (так называемая высота Солнца над горизонтом) в обоих случаях одинаков (для шеста и телеграфного столба), то треугольники ABC и DEF подобны по трем углам. Поэтому справедливо следующее соотношение:
Сделаем рисунок к задаче, на котором изобразим условно вертикально установленные шест и телеграфный столб (на рисунке AB и DE соответственно). Так как угол падения солнечных лучей (так называемая высота Солнца над горизонтом) в обоих случаях одинаков (для шеста и телеграфного столба), то треугольники ABC и DEF подобны по трем углам. Поэтому справедливо следующее соотношение:
\[\frac{h}{H} = \frac{l}{{l + \Delta l}}\]
Откуда имеем:
\[H = h\frac{{l + \Delta l}}{l}\]
Подставим численные данные задачи в полученную формулу и посчитаем ответ:
\[H = 1,1 \cdot \frac{{1,3 + 5,2}}{{1,3}} = 5,5\;м\]
Ответ: 5,5 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.1.19 Горизонтальный луч падает на плоское вертикально расположенное зеркало. На какой
10.1.21 На горизонтальном столе по прямой движется шарик. Под каким углом к плоскости стола
10.1.22 Плоское зеркало AB движется поступательно со скоростью v1=2 м/с, а точка S движется