Условие задачи:
Светящаяся точка равномерно движется по прямой, образующей угол 30° с плоскостью зеркала со скоростью 0,2 м/с. С какой скоростью изменяется расстояние между светящейся точкой и её изображением?
Задача №10.1.23 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha=30^\circ\), \(\upsilon=0,2\) м/с, \(u-?\)
Решение задачи:
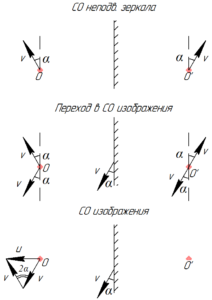 Вектор скорости изображения точки согласно правилу построения изображений в плоском зеркале будет симметричен вектору скорости предмета (светящейся точки) относительно плоскости зеркала.
Вектор скорости изображения точки согласно правилу построения изображений в плоском зеркале будет симметричен вектору скорости предмета (светящейся точки) относительно плоскости зеркала.
Чтобы ответить на вопрос задачи, то есть узнать с какой скоростью изменяется расстояние между точкой и её изображением (то есть найти скорость точки относительно изображения), перейдем в систему отсчета (СО) изображения точки. Для этого прибавим к векторам скоростей предмета (светящейся точки), зеркала и изображения предмета вектор, противоположный вектору скорости изображения.
Для нахождения искомой скорости точки \(\overrightarrow u\) относительно изображения нужно сложить два вектора \(\overrightarrow \upsilon\) с углом \(2\alpha\) между ними. Воспользуемся теоремой косинусов:
\[{u^2} = {\upsilon ^2} + {\upsilon ^2} — 2{\upsilon ^2}\cos 2\alpha \]
\[{u^2} = 2{\upsilon ^2} — 2{\upsilon ^2}\cos 2\alpha \]
\[{u^2} = 2{\upsilon ^2}\left( {1 — \cos 2\alpha } \right)\]
\[{u^2} = 2{\upsilon ^2} \cdot 2{\sin ^2}\alpha \]
\[u = 2\upsilon \sin \alpha \]
Численный ответ равен:
\[u = 2 \cdot 0,2 \cdot \sin 30^\circ = 0,2\;м/с\]
Ответ: 0,2 м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.1.22 Плоское зеркало AB движется поступательно со скоростью v1=2 м/с, а точка S движется
10.2.1 Показатель преломления воды для света с длиной волны в вакууме λ1=0,76 мкм
10.2.2 Как велика скорость света в алмазе?
Можно проще:
sin a=(u/2)/v;
(u/2)=v*sin a;
u=2*v*sina.
Согласен