Решение: Поверх стеклянной горизонтально расположенной пластины налит тонкий слой воды

Условие задачи:

Поверх стеклянной горизонтально расположенной пластины налит тонкий слой воды. Угол падения лучей света на поверхность воды равен 30°. Найти угол преломления лучей света, вышедших из стеклянной пластины.

Задача №10.3.30 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=30^\circ\), \(\delta-?\)

Решение задачи:

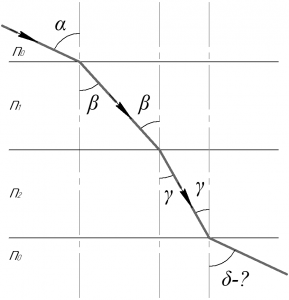Человек, знающий, что плоскопараллельная пластинка лишь смещает направление луча, должен сразу давать ответ на вопрос этой задачи. Но давайте докажем это, для чего запишем трижды закон преломления света (также известен как закон преломления Снеллиуса):

\[\left\{ \begin{gathered}
{n_0}\sin \alpha = {n_1}\sin \beta \hfill \\
{n_1}\sin \beta = {n_2}\sin \gamma \hfill \\
{n_2}\sin \gamma = {n_0}\sin \delta \hfill \\
\end{gathered} \right.\]

Здесь \(\alpha\), \(\beta\), \(\gamma\), \(\delta\) — углы падения и (или) преломления, \(n_0\), \(n_1\), \(n_2\) — показатели преломления сред.

Из записанной системы сразу видно, что:

\[{n_0}\sin \alpha = {n_0}\sin \delta \]

Значит:

\[\delta = \alpha \]

\[\delta = 30^\circ \]