Решение: Палка с изломом посередине погружена в пруд так, что наблюдателю, находящемуся

Условие задачи:

Палка с изломом посередине погружена в пруд так, что наблюдателю, находящемуся на берегу и смотрящему приблизительно вдоль надводной части палки, она кажется прямой, составляющей угол 30° с горизонтом. Какой угол излома имеет палка?

Задача №10.3.12 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\gamma=30^\circ\), \(\delta-?\)

Решение задачи:

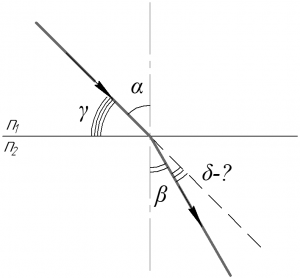Наблюдателю, смотрящему приблизительно вдоль надводной части палки с изломом, она покажется прямой, если палка повторяет ход светового луча (разумеется с такими же углами падения \(\alpha\) и преломления \(\beta\)). Из рисунка видно, что искомый угол излома палки \(\delta\) равен:

\[\delta = \alpha — \beta \;\;\;\;(1)\]

Так как наблюдателю палка кажется прямой, составляющей угол \(\gamma\) с горизонтом, то угол \(\alpha\) равен:

\[\alpha = 90^\circ — \gamma \;\;\;\;(2)\]

Чтобы найти угол \(\beta\), запишем закон преломления света (также известен как закон преломления Снеллиуса):

\[{n_1}\sin \alpha = {n_2}\sin \beta \]

Здесь \(\alpha\) и \(\beta\) — угол падения и угол преломления соответственно, \(n_1\) и \(n_2\) — показатели преломления сред. Показатель преломления воздуха \(n_1\) равен 1, показатель преломления воды \(n_2\) равен 1,33.

Тогда:

\[\sin \beta = \frac{{{n_1}\sin \alpha }}{{{n_2}}}\]

\[\beta = \arcsin \left( {\frac{{{n_1}\sin \alpha }}{{{n_2}}}} \right)\]

Учитывая (2), имеем:

\[\beta = \arcsin \left( {\frac{{{n_1}\sin \left( {90^\circ — \gamma } \right)}}{{{n_2}}}} \right)\;\;\;\;(3)\]

Подставим выражения (2) и (3) в формулу (1):

\[\delta = 90^\circ — \gamma — \arcsin \left( {\frac{{{n_1}\sin \left( {90^\circ — \gamma } \right)}}{{{n_2}}}} \right)\]

Посчитаем численный ответ данной задачи:

\[\delta = 90^\circ — 30^\circ — \arcsin \left( {\frac{{1 \cdot \sin \left( {90^\circ — 30^\circ } \right)}}{{1,33}}} \right) = 19,4^\circ \]