Решение: Горизонтальный луч падает на плоское вертикально расположенное зеркало. На какой

Условие задачи:

Горизонтальный луч падает на плоское вертикально расположенное зеркало. На какой угол необходимо повернуть зеркало вокруг вертикальной оси, чтобы отраженный луч повернулся на 30°?

Задача №10.1.19 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=30^\circ\), \(\beta-?\)

Решение задачи:

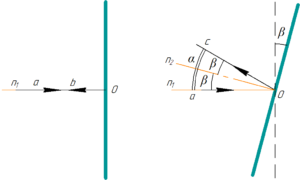Так как изначально горизонтальный луч a падает на вертикальное зеркало, то есть угол падения этого луча равен 0°, то он отражается обратно в том же направлении (см. луч b на левой части рисунка к задаче), поскольку согласно закону отражения света угол падения луча равен углу отражения.

Далее зеркало поворачивают на какой-то угол так, что отраженный луч (луч c) поворачивается на угол \(\alpha\) (мы поворачиваем по часовой стрелке, см. правую часть рисунка). Биссектриса угла между лучами a и c (так как угол падения равен углу отражения) есть новое положение нормали n₂. Перпендикулярно этой новой нормали и располагается зеркало. Искомый угол поворота зеркала есть угол поворота нормали, то есть угол между n₁ и n₂. Из рисунка видно, что:

\[\alpha = 2\beta \]

\[\beta = \frac{\alpha }{2}\]

Численный ответ равен:

\[\beta = \frac{{30^\circ }}{2} = 15^\circ \]