Решение: Определить радиус колеса, если при вращении скорость точек на ободе колеса

Условие задачи:

Определить радиус колеса, если при вращении скорость точек на ободе колеса равна 10 м/с, а скорость точек, лежащих на 42 см ближе к оси, 4 м/с.

Задача №1.8.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon_1=10\) м/с, \(\Delta R=42\) см, \(\upsilon_2=4\) м/с, \(R-?\)

Решение задачи:

Линейная скорость любой точки колеса в общем виде определяется по формуле:

\[\upsilon = \omega R\]

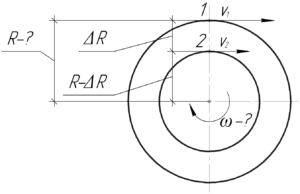
В этой формуле \(\omega\) – угловая скорость вращения колеса, \(R\) – расстояние от оси вращения до нужной точки. Учитывая все вышесказанное, запишем систему (смотри рисунок):

\[\left\{ \begin{gathered}
{\upsilon _1} = \omega R \;\;\;\;(1)\hfill \\
{\upsilon _2} = \omega \left( {R – \Delta R} \right) \;\;\;\;(2)\hfill \\
\end{gathered} \right.\]

Делим выражение (1) на выражение (2).

\[\frac{{{\upsilon _1}}}{{{\upsilon _2}}} = \frac{R}{{R – \Delta R}}\]

Перемножим “крест-накрест”, тогда получим следующее уравнение.

\[{\upsilon _1}R – {\upsilon _1}\Delta R = {\upsilon _2}R\]

В левую сторону переносим все члены с \(R\), в правую – без \(R\), выносим в левой части общий множитель \(R\) и выражаем его.

\[{\upsilon _1}R – {\upsilon _2}R = {\upsilon _1}\Delta R\]

\[R\left( {{\upsilon _1} – {\upsilon _2}} \right) = {\upsilon _1}\Delta R\]

\[R = \frac{{{\upsilon _1}\Delta R}}{{{\upsilon _1} – {\upsilon _2}}}\]

Переведем расстояние \(\Delta R\) из см в м (то есть в систему СИ).

\[42\; см = \frac{{42}}{{100}}\; м = 0,42\; м\]

Подставим исходные данные задачи в полученную формулу, сосчитав, получим ответ.

\[R = \frac{{10 \cdot 0,42}}{{10 – 4}} = 0,7\; м\]