Условие задачи:
В электронно-лучевой трубке поток электронов с кинетической энергией 8 кэВ движется между пластинами плоского конденсатора длиной 4 см. Расстояние между пластинами 2 см. Какое напряжение нужно подать на пластины конденсатора, чтобы смещение электронного пучка на выходе оказалось 8 мм?
Задача №6.3.53 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(W_к=8\) кэВ, \(l=4\) см, \(d=2\) см, \(\delta = 8\) мм, \(U-?\)
Решение задачи:
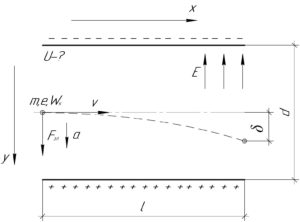 При нахождении электрона между обкладками конденсатора на него действует одна сила – электрическая сила \(F_{эл}\), направленная вдоль оси \(y\), модуль которой мы найдём по формуле:
При нахождении электрона между обкладками конденсатора на него действует одна сила – электрическая сила \(F_{эл}\), направленная вдоль оси \(y\), модуль которой мы найдём по формуле:
\[F_{эл} = Ee\]
В этой формуле \(e\) – модуль заряда электрона (элементарный заряд), равный 1,6·10-19 Кл.
Напряженность поля конденсатора \(E\) можно выразить через искомое напряжение между пластинами \(U\) и расстояние между ними \(d\):
\[E = \frac{U}{d}\]
Тогда:
\[{F_{эл}} = \frac{{Ue}}{d}\;\;\;\;(1)\]
Запишем второй закон Ньютона для электрона (одного из потока) в проекции на ось \(y\):
\[{F_{эл}} = ma\;\;\;\;(2)\]
Здесь \(m\) – масса электрона, равная 9,1·10-31 кг. Приравняем (1) и (2), тогда:
\[\frac{{Ue}}{d} = ma\]
\[U = \frac{{mad}}{e}\;\;\;\;(3)\]
Получается, что нам нужно определить ускорение \(a\), действующее на электрон. Для этого запишем уравнения движения электрона вдоль осей координат. Вдоль оси \(x\) электрон движется равномерно (так как вдоль этой оси на него не действует сил), а вдоль оси \(y\) – равноускоренно (из-за электрической силы \(F_{эл}\)).
\[\left\{ \begin{gathered}
x = \upsilon t \hfill \\
y = \frac{{a{t^2}}}{2} \hfill \\
\end{gathered} \right.\]
Пусть \(t\) – время нахождения электрона в конденсаторе. За это время электрон вдоль оси \(x\) пройдёт путь, равный длине обкладок \(l\), а вдоль оси \(y\) – путь, равный смещению пучка \(\delta\), поэтому вышеприведённая система примет вид:
\[\left\{ \begin{gathered}
l = \upsilon t \hfill \\
\delta = \frac{{a{t^2}}}{2} \hfill \\
\end{gathered} \right.\]
Из нижнего уравнения системы имеем:
\[a = \frac{2 \delta}{{{t^2}}}\;\;\;\;(4)\]
Из верхнего уравнения выразим время движения \(t\) и возведём его в квадрат:
\[t = \frac{l}{\upsilon } \Rightarrow {t^2} = \frac{{{l^2}}}{{{\upsilon ^2}}}\]
Тогда формула (4) станет такой:
\[a = \frac{{{2 \delta \upsilon ^2}}}{{{l^2}}}\;\;\;\;(5)\]
В условии сказано, что энергия электронов равна \(W_к\), поэтому мы легко можем определить скорость электрона \(\upsilon\) при влёте в конденсатор (вернее нам нужен квадрат скорости \(\upsilon^2\)).
\[{W_к} = \frac{{m{\upsilon ^2}}}{2}\]
\[{\upsilon ^2} = \frac{{2{W_к}}}{m}\]
Полученное выражение подставим в формулу (5):
\[a = \frac{{2\delta }}{{{l^2}}} \cdot \frac{{2{W_к}}}{m}\]
\[a = \frac{{4{W_к}\delta }}{{m{l^2}}}\]
Осталось это выражение подставить в формулу (3):
\[U = \frac{{md}}{e} \cdot \frac{{4{W_к}\delta }}{{m{l^2}}}\]
\[U = \frac{{4\delta d{W_к}}}{{e{l^2}}}\]
Задача решена в общем виде. Теперь нужно поставить численные значения величин и посчитать численный ответ (помните, что 1 эВ = 1,6·10-19 Дж):
\[U = \frac{{4 \cdot 0,008 \cdot 0,02 \cdot 8 \cdot {{10}^3} \cdot 1,6 \cdot {{10}^{ – 19}}}}{{1,6 \cdot {{10}^{ – 19}} \cdot {{0,04}^2}}} = 3200\;В = 3,2\;кВ\]
Ответ: 3,2 кВ.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.3.52 Маленький металлический шарик массой 1 г и зарядом 100 нКл брошен издалека
6.3.54 В закрепленной металлической сфере радиусом 1 см, имеющей заряд -10 нКл
6.3.55 В зазор между пластинами плоского конденсатора влетает электрон, пройдя перед