Условие задачи:
Охотник стреляет с легкой надувной лодки, находящейся в покое. Какую скорость приобретает лодка в момент выстрела, если масса охотника с лодкой 70 кг, масса дроби 35 г, начальная скорость дроби 320 м/с? Ствол ружья во время выстрела направлен под углом 60° к горизонту. Сопротивлением воды пренебречь.
Задача №2.10.7 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(M=70\) кг, \(m=35\) г, \(\upsilon_0=320\) м/с, \(\alpha=60^\circ\), \(u-?\)
Решение задачи:
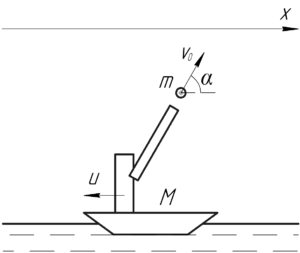На систему тел, данных в задаче (лодка, охотник, ружье и дробь), вдоль оси \(x\) не действуют никакие силы, значит эта система тел замкнута вдоль этой оси. Поэтому запишем закон сохранения импульса в проекции на ось \(x\):
\[0 = m{\upsilon _0}\cos \alpha – Mu\]
Выразим скорость лодки \(u\) после выстрела:
\[u = \frac{{m{\upsilon _0}\cos \alpha }}{M}\]
Переведем массу дроби в систему СИ, так как в условии она дана в граммах.
\[35\; г = \frac{{35}}{{1000}}\; кг = 0,035\; кг\]
Подставим исходные данные в последнюю формулу и посчитаем ответ:
\[u = \frac{{0,035 \cdot 320 \cdot \cos 60^\circ }}{{70}} = 0,08\; м/с = 0,29\; км/ч\]
Ответ: 0,29 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.10.6 Два шара массами 0,3 и 0,2 кг движутся навстречу друг другу. Скорость первого шара
2.10.8 Груз массой 0,5 кг падает с некоторой высоты на плиту массой 1 кг, укрепленную
2.10.9 Масса пушки 800 кг. Пушка выстреливает ядро массой 10 кг с начальной скоростью
Задача аналогичная. Какая скорость после трёх выстрелов
Закон сохранения импульса в проекции на ось \(x\):\[0 = 3m{\upsilon _0}\cos \alpha – Mu\]Откуда:\[u = \frac{{3m{\upsilon _0}\cos \alpha }}{M}\]Численный ответ:\[u = \frac{{3 \cdot 0,035 \cdot 320 \cdot \cos 60^\circ }}{{70}} = 0,24\;м/с\]
ответ не верный решение правильное
Почему? Аргументируйте
возможно, вместо косинуса стоит поставить sin, так как проекция на ось x, а не на ось y
Окей, допустим Вы правы, т.е. проекция скорости на ось \(x\) равна \({\upsilon _0}\sin \alpha \). Вы должны понимать, что это выражение справедливо для любого значения угла \(\alpha\). Возьмем (чтобы доказать, что Вы не правы) угол 0°, т.е. горизонтальное направление скорости \(\upsilon_0\). Очевидно, что проекция скорости на ось \(x\) равна \(\upsilon_0\), т.к. скорость сонаправлена с осью. А вот по Вашей формуле проекция скорости будет равна нулю (так как синус нуля равен нулю). Противоречие налицо.
Подскажите, какой материал надо прочитать, чтобы понимать откуда берется выражение mV*cos(a)?
Почитайте про проецирование векторов