Условие задачи:

Тело, имея начальную скорость 1 м/с, двигаясь равноускоренно, приобрело, пройдя некоторое расстояние, скорость 7 м/с. Какова была скорость тела на половине этого расстояния?

Задача №1.3.47 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$\upsilon_0=1$ м/с, $\upsilon=7$ м/с, $S_1=\frac{1}{2}S$, $\upsilon_1-?$

Решение задачи:

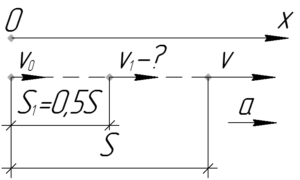Запишем систему из двух уравнений, первое — для полного пути $S$, второе — для его половины $S_1$. Каждое уравнение — это известная формула кинематики.

$$\left\{ \begin{gathered} {\upsilon ^2} — \upsilon _0^2 = 2aS \hfill \\ \upsilon _1^2 — \upsilon _0^2 = 2a{S_1} \hfill \\ \end{gathered} \right.$$

Разделим уравнения друг на друга.

$$\frac{{\upsilon _1^2 — \upsilon _0^2}}{{{\upsilon ^2} — \upsilon _0^2}} = \frac{{{S_1}}}{S}$$

Так как по условию $\frac{{{S_1}}}{S} = \frac{1}{2}$, то:

$$\frac{{\upsilon _1^2 — \upsilon _0^2}}{{{\upsilon ^2} — \upsilon _0^2}} = \frac{1}{2}$$

Перемножаем крест-накрест.

$$2\upsilon _1^2 — 2\upsilon _0^2 = {\upsilon ^2} — \upsilon _0^2$$

$$2\upsilon _1^2 = {\upsilon ^2} + \upsilon _0^2$$

$$\upsilon _1^2 = \frac{{{\upsilon ^2} + \upsilon _0^2}}{2}$$

После всех преобразований Вы должны получить такую окончательную формулу:

$${\upsilon _1} = \sqrt {\frac{{{\upsilon ^2} + \upsilon _0^2}}{2}}$$

Сосчитаем ответ:

$${\upsilon _1} = \sqrt {\frac{{{7^2} + {1^2}}}{2}}  = 5\; м/с = 18\; км/ч$$

Ответ: 18 км/ч.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.3.46 Тело, двигаясь с начальной скоростью 10 м/с и постоянным ускорением 10 м/с2
1.3.48 Прямолинейное движение точки задано уравнением x=-2+3t-0,5t^2 (м). Найти
1.3.49 Пуля, летящая со скоростью 141 м/с, попадает в доску и проникает на глубину