Условие задачи:

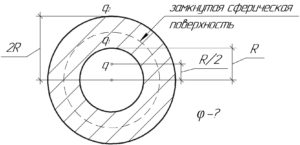
Внутри шарового металлического слоя, внутренний и внешний радиусы которого соответственно равны R и 2R, на расстоянии R/2 от центра находится точечный положительный заряд q. Найти потенциал в центре сферы.

Задача №6.3.59 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(R\), \(2R\), \(\frac{R}{2}\), \(q\), \(\varphi-?\)

Решение задачи:

Шаровой слой изготовлен из металла, значит он является проводником — это очень важный факт, он нам пригодится для решения этой интересной задачи.

Вы должны понимать, что под воздействием заряда \(q\) свободные заряды (электроны), содержащиеся в шаровом сегменте, должны были прийти в движение и распределиться каким-то образом по внешней и внутренней поверхности этого слоя. Распределение зарядов по этим поверхностям будет далеко не равномерным, поскольку заряд \(q\) находится не в центре шарового слоя. Но одно мы знаем точно — напряженность поля внутри проводника должна быть равна нулю, иначе в противном случае возникнут условия для движения этих свободных зарядов.

Для решения этой задачи нужно применить теорему Гаусса. Согласно этой теореме поток вектора напряженности через любую замкнутую поверхность равен алгебраической сумме зарядов, находящихся внутри этой поверхности, делённой на электрическую постоянную. Аналитически это записывается в таком виде:

\[\Phi = \frac{q}{{{\varepsilon _0}}}\;\;\;\;(1)\]

Чтобы дать определение потоку вектора напряженности \(\Phi\), дадим определение элементарному потоку вектора напряженности \(\Delta \Phi\) через малую площадку — это произведение модуля вектора напряженности поля \(E\) на площадь этой площадки \(\Delta S\) и косинус угла \(\alpha\) между вектором напряженности поля и нормалью к этой площадке, то есть:

\[\Delta \Phi = E \cdot \Delta S \cdot \cos \alpha \;\;\;\;(2)\]

Поток вектора напряженности \(\Phi\) через замкнутую поверхность равен сумме элементарных потоков через все её участки, то есть:

\[\Phi = \sum {\Delta \Phi } \;\;\;\;(3)\]

Пусть заряд на внутренней поверхности слоя равен \(q_1\), а на внешней — \(q_2\). Выделим замкнутую сферическую поверхность, находящуюся внутри слоя (смотрите схему). Мы уже говорили, что напряженность поля внутри шарового слоя равна нулю, поэтому, используя формулы (2) и (3), нетрудно догадаться, что поток вектора напряженности \(\Phi\) через замкнутую поверхность также равен нулю, значит и сумма зарядов внутри этой поверхности согласно формуле (1) равна нулю. А какие заряды находятся внутри сферической поверхности? Правильно, это заряд \(q\) и заряд на внутренней поверхности слоя равен \(q_1\). Значит:

\[q + {q_1} = 0\]

\[{q_1} = — q\;\;\;\;(4)\]

Изначально, то есть до внесения заряда \(q\), шаровой слой не был заряжен (в условии не говорится об обратном), значит заряд шарового слоя был равен нулю. После внесения заряда \(q\) в шаровом слое произошло перераспределение зарядов, но их сумма также осталась равной нулю, поскольку слою не передавали заряда. Поэтому:

\[{q_1} + {q_2} = 0\]

\[{q_2} = — {q_1}\]

Учитывая (4), имеем:

\[{q_2} = q\]

Наконец, перейдём к главному вопросу этой задачи — нахождению потенциала в центре слоя. Поскольку потенциал — величина скалярная, то искомый потенциал \(\varphi\) будем находить таким образом:

\[\varphi = {\varphi _1} + {\varphi _2} + {\varphi _3}\;\;\;\;(5)\]

Потенциал в центре слоя \(\varphi_1\) от заряда \(q\) легко найти по следующей известной формуле:

\[{\varphi _1} = \frac{{kq}}{{\frac{R}{2}}} = \frac{{2kq}}{R}\;\;\;\;(6)\]

Заряд \(-q\) распределен по внутренней поверхности шарового слоя неравномерно. Чтобы найти потенциал в центре слоя \(\varphi_2\), создаваемый этим зарядом, выделим маленькую площадку на внутренней поверхности и рассмотрим элементарный заряд \(\Delta q_i\). Поскольку эта площадка находится на расстоянии \(R\) от центра слоя, то этот элементарный заряд будет создавать в центре слоя потенциал \(\Delta \varphi_i\), равный:

\[\Delta {\varphi _i} = \frac{{k\Delta {q_i}}}{R}\]

Если сложить потенциал от всех таких элементарных зарядов \(\Delta q_i\) (не думайте, что они одинаковы по величине, ведь заряд распределен неравномерно!), то получим потенциал \(\varphi_2\):

\[{\varphi _2} = \sum {\frac{{k\Delta {q_i}}}{R}} = \frac{k}{R}\sum {\Delta {q_i}} \]

Понятно, что сумма элементарных зарядов \(\Delta q_i\) на внутренней поверхности равна \(-q\), поэтому:

\[{\varphi _2} = \frac{{ — kq}}{R}\;\;\;\;(7)\]

Рассуждая таким же образом, можно найти и потенциал \(\varphi_3\), создаваемый зарядом \(q\), распределённым по внешней поверхности сферы (учтите, то любой заряд на внешней поверхности расположен на расстоянии \(2R\) от центра):

\[{\varphi _3} = \frac{{kq}}{{2R}}\;\;\;\;(8)\]

Подставим (6)-(8) в (5), тогда:

\[\varphi = \frac{{2kq}}{R} + \left( {\frac{{ — kq}}{R}} \right) + \frac{{kq}}{{2R}}\]

\[\varphi = \frac{{3kq}}{{2R}}\]

Ответ также можно представить в другом виде (\(k = \frac{1}{{4\pi {\varepsilon _0}}}\)):

\[\varphi = \frac{{3q}}{{8\pi {\varepsilon _0}R}}\]

Ответ: \(\varphi = \frac{{3q}}{{8\pi {\varepsilon _0}R}}\).

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.3.58 Шарик массой 10 г с зарядом 100 мкКл подвешен на тонкой нити длиной 50 см
6.3.60 По тонкому проволочному кольцу радиуса 3 см равномерно распределен заряд 10^(-9) Кл
6.3.61 Какую работу необходимо совершить, чтобы три одинаковых точечных положительных