Условие задачи:

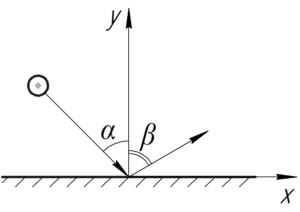При ударе шарика об идеально гладкую горизонтальную поверхность теряется третья часть его кинетической энергии. Зная, что угол падения $\alpha=45^\circ$, найти угол отражения $\beta$.

Задача №2.8.52 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$\alpha=45^\circ$, $\gamma=\frac{1}{3}$, $\beta-?$

Решение задачи:

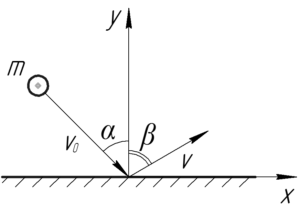На шарик вдоль оси $x$ не действует никаких сил, т.е. система замкнута вдоль этой оси, поэтому можем записать закон сохранения импульса в проекции на эту ось.

$$m{\upsilon _0}\sin \alpha  = m\upsilon \sin \beta$$

$$\beta  = \arcsin \left( {\frac{{{\upsilon _0}\sin \alpha }}{\upsilon }} \right)\;\;\;\;(1)$$

Здесь $m$ — это масса шарика. Обратите внимание, что скорость шарика до и после удара разная, так как часть кинетической энергии теряется — удар был неупругий. Для неупругого удара можно применять закон сохранения энергии, но нужно не забывать о переходе части начальной энергии в энергию деформации (или внутреннюю энергию).

$$\frac{{m\upsilon _0^2}}{2} = \frac{{m{\upsilon ^2}}}{2} + Q$$

Поделим это равенство на начальную энергию $\frac{{m\upsilon _0^2}}{2}$, тогда:

$$1 = {\left( {\frac{\upsilon }{{{\upsilon _0}}}} \right)^2} + \frac{{2Q}}{{m\upsilon _0^2}}$$

Дробь $\frac{{2Q}}{{m\upsilon _0^2}}$ равна $\gamma$ по условию задачи:

$$1 = {\left( {\frac{\upsilon }{{{\upsilon _0}}}} \right)^2} + \gamma$$

$$\frac{\upsilon }{{{\upsilon _0}}} = \sqrt {1 — \gamma }$$

Последнее выражение подставим в формулу (1), тогда получим решение задачи в общем виде:

$$\beta  = \arcsin \left( {\frac{{\sin \alpha }}{{\sqrt {1 — \gamma } }}} \right)$$

Посчитаем ответ:

$$\beta  = \arcsin \left( {\frac{{\sin 45^\circ }}{{\sqrt {1 — \frac{1}{3}} }}} \right) = 60^\circ  = \frac{\pi }{3}$$

Ответ: $\frac{\pi }{3}$.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.8.51 Подвешенному на нити длиной 1 м шарику сообщили начальную скорость такую
2.8.53 Шарик на нити отклонили от вертикали на 60 градусов и отпустили без начальной
2.9.1 Тело массой 1 кг упруго ударяется о покоящееся тело массой 3 кг и летит обратно