Условие задачи:
На горизонтальном столе лежит деревянный брусок массой 5 кг. В брусок попадает пуля массой 9 г, после чего он проходит по столу расстояние 25 см и останавливается. Коэффициент трения 0,25. Найти скорость пули.
Задача №2.10.21 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(M=5\) кг, \(m=9\) г, \(S=25\) см, \(\mu=0,25\), \(\upsilon_0-?\)
Решение задачи:
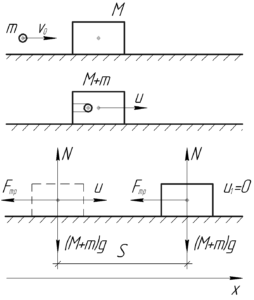 Поскольку в этой задаче мы имеем дело с абсолютно неупругим ударом, то запишем закон сохранения импульса в проекции на ось \(x\):
Поскольку в этой задаче мы имеем дело с абсолютно неупругим ударом, то запишем закон сохранения импульса в проекции на ось \(x\):
\[m{\upsilon _0} = \left( {m + M} \right)u\]
Выразим из полученного равенства скорость пули \(\upsilon_0\):
\[{\upsilon _0} = \frac{{\left( {m + M} \right)u}}{m}\;\;\;\;(1)\]
Брусок с пулей внутри, имея после удара скорость \(u\), пройдет до остановки расстояние \(S\). Применим такую формулу из кинематики:
\[0 — {u^2} = — 2aS\]
\[u = \sqrt {2aS} \;\;\;\;(2)\]
Как видно, нам необходимо узнать ускорение — это можно сделать с помощью второго закона Ньютона, записанного в проекции на ось \(x\). На рассматриваемое тело действует только сила трения скольжения, поэтому:
\[ — {F_{тр}} = — \left( {M + m} \right)a\]
\[{F_{тр}} = \left( {M + m} \right)a\]
Саму силу трения скольжения определим по формуле:
\[{F_{тр}} = \mu N = \mu \left( {M + m} \right)g\]
Приравнивая две последние приведенные формулы, получим:
\[\left( {M + m} \right)a = \mu \left( {M + m} \right)g\]
\[a = \mu g\;\;\;\;(3)\]
Подставим (3) в (2), а полученное в (1):
\[{\upsilon _0} = \frac{{\left( {m + M} \right)}}{m}\sqrt {2\mu gS} \]
Задача решена в общем виде. Перед тем как подставлять числа в формулу, переведем некоторые из них в систему СИ:
\[9\; г = \frac{9}{{1000}}\; кг = 0,009\; кг\]
\[25\; см = \frac{{25}}{{100}}\; м = 0,25\; м\]
Считаем ответ:
\[{\upsilon _0} = \frac{{\left( {0,009 + 5} \right)}}{{0,009}}\sqrt {2 \cdot 0,25 \cdot 10 \cdot 0,25} = 622,25\; м/с\]
Ответ: 622,25 м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.10.20 Кусок пластилина массой m=32 г попадает в брусок массой 6m, двигавшийся
2.10.22 По горизонтальной поверхности стола скользит брусок массой m и сталкивается
2.10.23 Пуля массой 10 г застревает в первоначально покоящемся бруске, масса которого 0,1 кг
спасибо оч круто