Условие задачи:
Маленький шарик, подвешенный на нити, движется по окружности так, что нить составляет с вертикалью постоянный угол 30°. Другой такой же шарик, подвешенный на нити такой же длины, движется так, что его нить составляет с вертикалью постоянный угол 45°. Во сколько раз кинетическая энергия второго шарика больше, чем первого?
Задача №2.4.31 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha = 30^\circ\), \(\beta=45^\circ\), \(\frac{E_{к2}}{E_{к1}}-?\)
Решение задачи:
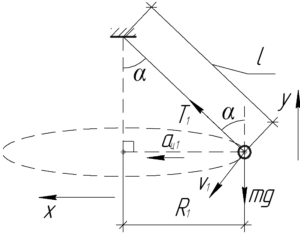 Очевидно, что отношение кинетических энергий шариков будет равно отношению квадратов скоростей шариков, поскольку их массы одинаковы.
Очевидно, что отношение кинетических энергий шариков будет равно отношению квадратов скоростей шариков, поскольку их массы одинаковы.
\[\frac{{{E_{к2}}}}{{{E_{к1}}}} = \frac{{\upsilon _2^2}}{{\upsilon _1^2}}\;\;\;\;(1)\]
Смысла рассматривать оба шарика нет – достаточно рассмотреть только первый (для него и приведен рисунок). Запишем первый закон Ньютона в проекции на ось \(y\) и второй закон Ньютона в проекции на ось \(x\):
\[\left\{ \begin{gathered}
T_1 \cdot \cos \alpha = mg \hfill \\
T_1 \cdot \sin \alpha = m{a_{ц1}} \hfill \\
\end{gathered} \right.\]
Если первый шарик движется равномерно по окружности со скоростью \(\upsilon\), то действующее на него центростремительное ускорение \(a_ц\) равно:
\[{a_{ц1}} = \frac{{\upsilon _1^2}}{R_1}\]
Система примет такой вид:
\[\left\{ \begin{gathered}
T_1 \cdot \cos \alpha = mg \hfill \\
T_1 \cdot \sin \alpha = m\frac{{\upsilon _1^2}}{R_1} \hfill \\
\end{gathered} \right.\]
Поделим нижнее равенство на верхнее, тогда:
\[tg\alpha = \frac{{\upsilon _1^2}}{{g{R_1}}}\]
На схеме видно, что радиус \(R_1\) равен:
\[{R_1} = l \cdot \sin \alpha \]
\[tg\alpha = \frac{{\upsilon _1^2}}{{gl \cdot \sin \alpha }}\]
\[\upsilon _1^2 = gl \cdot \sin \alpha \cdot tg\alpha \;\;\;\;(2)\]
Для второго шарика, произведя аналогичные действия, вы получите:
\[\upsilon _2^2 = gl \cdot \sin \beta \cdot tg\beta \;\;\;\;(3)\]
Подставим полученные выражения (2) и (3) в (1), тогда:
\[\frac{{{E_{к2}}}}{{{E_{к1}}}} = \frac{{gl \cdot \sin \beta \cdot tg\beta }}{{gl \cdot \sin \alpha \cdot tg\alpha }}\]
\[\frac{{{E_{к2}}}}{{{E_{к1}}}} = \frac{{\sin \beta \cdot tg\beta }}{{\sin \alpha \cdot tg\alpha }}\]
Осталось посчитать ответ:
\[\frac{{{E_{к2}}}}{{{E_{к1}}}} = \frac{{\sin 45^\circ \cdot tg45^\circ }}{{\sin 30^\circ \cdot tg30^\circ }} = 2,45\]
Ответ: в 2,45 раза.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.4.30 Какова должна быть максимальная длина выпуклого симметричного относительно
2.4.32 Мотоциклист движется по цилиндрической стенке диаметра 12 м. При каком коэффициенте
2.4.33 Спортивный молот – ядро на тросике длиной L, бросают, раскрутив вокруг себя
Как мы определили оси x и y в самом начале??
Выбрал удобное (для себя) расположение указанных осей