Условие задачи:
Какова должна быть максимальная длина выпуклого симметричного относительно вертикали моста радиусом 100 м, чтобы автомобиль мог проходить по нему со скоростью 90 км/ч, не отрываясь от полотна дороги?
Задача №2.4.30 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(R=100\) м, \(\upsilon=90\) км/ч, \(L-?\)
Решение задачи:
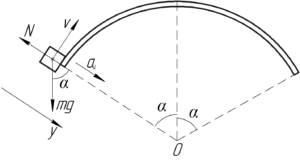 Рассмотрим произвольное положение автомобиля на выпуклом мосте. На него действуют сила тяжести \(mg\) и сила реакции опоры \(N\). Запишем второй закон Ньютона в проекции на ось \(y\) (смотрите схему):
Рассмотрим произвольное положение автомобиля на выпуклом мосте. На него действуют сила тяжести \(mg\) и сила реакции опоры \(N\). Запишем второй закон Ньютона в проекции на ось \(y\) (смотрите схему):
\[mg \cdot \cos \alpha — N = m{a_ц}\]
Если в рассматриваемой точке автомобиль имеет скорость \(\upsilon\), то центростремительное ускорение \(a_ц\), действующее на автомобиль, можно найти по формуле:
\[{a_ц} = \frac{{{\upsilon ^2}}}{R}\]
Если в этой точке автомобиль отрывается от полотна, то сила реакции \(N\) будет равна нулю. Учитывая вышесказанное, имеем:
\[mg \cdot \cos \alpha = m\frac{{{\upsilon ^2}}}{R}\]
\[g \cdot \cos \alpha = \frac{{{\upsilon ^2}}}{R}\]
\[\cos \alpha = \frac{{{\upsilon ^2}}}{{gR}}\;\;\;\;(1)\]
При этом скорость автомобиля \(\upsilon\) можно определить из формулы:
\[\upsilon = \sqrt {gR \cdot \cos \alpha } \]
По сути мы нашли формулу, которая показывает максимальную скорость движения автомобиля без отрыва от полотна в произвольной точке. Эта точка на окружности моста определяется углом \(\alpha\). Получается, что чем больше угол \(\alpha\), тем меньше допустимая скорость. Значит, что скорее всего автомобиль оторвется от полотна при въезде на мост, чем в его середине (смотрите схему).
Из равенства (1) выразим угол \(\alpha\):
\[\alpha = \arccos \left( {\frac{{{\upsilon ^2}}}{{gR}}} \right)\]
Зная угол \(\alpha\), легко найти длину моста по следующей формуле (учтите, что угол в эту формулу подставляется в радианах, поэтому калькулятор должен быть настроен на RAD):
\[L = 2\alpha R\]
\[L = 2R \cdot \arccos \left( {\frac{{{\upsilon ^2}}}{{gR}}} \right)\]
Переведем скорость в систему СИ, потом посчитаем ответ:
\[90\; км/ч = \frac{{90 \cdot 1000}}{{1 \cdot 3600}}\; м/с = \frac{{900}}{{36}}\; м/с = 25\; м/с\]
\[L = 2 \cdot 100 \cdot \arccos \left( {\frac{{{{25}^2}}}{{10 \cdot 100}}} \right) = 179\; м\]
Ответ: 179 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.4.29 К потолку лифта на нити длиной 40 см прикреплен шар массой 800 г, который вращается
2.4.31 Маленький шарик, подвешенный на нити, движется по окружности так, что нить
2.4.32 Мотоциклист движется по цилиндрической стенке диаметра 12 м. При каком коэффициенте
«Если в этой точке автомобиль отрывается от полотна, то сила реакции N будет равна нулю»
А зачем так делать?
Это условие отрыва автомобиля от полотна дороги
откуда в 1) взялось 2 gR в знаменателе?
Двойки там быть не должно, это опечатка, я исправил
я не понял почему там arccos а не 1/arccos? разве он не должен рядом c g
Специально для Вас я дополнил решение, ещё более подробно расписав, как я нашёл угол α