Условие задачи:
При подвеске контактного провода троллейбусной сети провес опорного троса не должен превышать 0,50 м. Определить силу натяжения троса, если его длина 30 м, а вес контактного провода, присоединенного посредине троса, 230 Н.
Задача №3.1.12 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(h=0,5\) м, \(l=30\) м, \(P=230\) Н, \(T-?\)
Решение задачи:
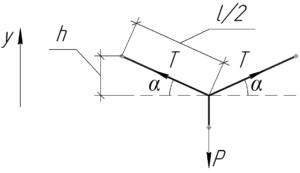Поскольку контактный провод подвешивают посередине опорного троса, то схема получается симметричной, и силы натяжения троса по обе стороны равны (смотрите схему). Запишем первое условие равновесия контактного провода в проекции на ось \(y\):
\[T \cdot \sin \alpha + T \cdot \sin \alpha = P\]
\[2T \cdot \sin \alpha = P\]
\[T = \frac{P}{{2\sin \alpha }}\]
Воспользуемся схемой, чтобы найти синус угла \(\alpha\). Очевидно, что:
\[\sin \alpha = \frac{{2h}}{l}\]
Тогда:
\[T = \frac{{Pl}}{{4h}}\]
Численное значение силы натяжения опорного троса равно:
\[T = \frac{{230 \cdot 30}}{{4 \cdot 0,5}} = 3450\;Н = 3,45\;кН\]
Ответ: 3,45 кН.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.1.11 На двух взаимно перпендикулярных наклонных плоскостях, из которых одна наклонена
3.1.13 Два шара, алюминиевый и цинковый, одинакового объема и радиуса 10 см скреплены
3.1.14 Три однородных шара массой 1, 2 и 2 кг укреплены на легко стержне. Центр 2-ого шара
Спасибо большое.
Простите, но не соглашусь с нахождением синуса, у вас вся нить L, когда мы берем за ее серединку и прогибаем ее вниз, 2 частички уже не по L/2, это уже будет гипотенуза в прямоугольном треугольнике с катетом H и вторым катетом(нижний) L/2 итого ваш кусочек будет квадратный корень из суммы квадратов этих двух катетов, но никак не просто L/2.
Вообще, если опорный трос нерастяжим, то говоря “у вас вся нить L, когда мы берем за ее серединку и прогибаем ее вниз, 2 частички уже не по L/2” Вы противоречите сами себе – если берете за середину, то с чего бы двум получившимся частям не быть по половине? Ну а если он растяжим, то в условии не указан коэффициент упругости и другие физические и геометрические параметры троса, исходя из которых мы могли бы указанный коэффициент найти.
Также, исходя из Ваших рассуждений, то L – это расстояние между опорами опорного троса (извините за тавтологию), а в условии явно сказано, что L – это длина опорного троса (вообще, мне следовало бы с этого и начинать ответ на Ваш комментарий).
Да, я про растяжимость говорил.
А как тогда если был бы коэффициент, прилепить его сюда?
Хм, нет, про коэффициент я лишнего сказал, извините.
В случае растяжимого троса Вас бы попросили найти силу упругости. Всё осталось бы также, только вот синус уже искали так, как Вы и сами предложили.
Но в условии явно сказано, что L — это длина опорного троса, так что такой случай не имеет права на жизнь (по моему мнению). А длина троса не может быть равна расстоянию между опорами, потому что трос всё-таки вешают с провисом.