Условие задачи:
Лестница массой 15 кг и длиной 3 м стоит, упираясь верхним концом в гладкую стену, а нижним — в пол под углом 60° к горизонту. На лестнице на расстоянии 1 м от её верхнего конца стоит человек массой 60 кг. Под каким углом к горизонту направлена сила, с которой пол действует на нижний конец лестницы?
Задача №3.1.22 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=15\) кг, \(L=3\) м, \(\alpha=60^\circ\), \(l=1\) м, \(M=60\) кг, \(\beta — ?\)
Решение задачи:
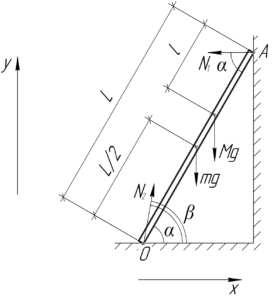 На лестницу действуют следующие силы: сила тяжести лестницы \(mg\), сила тяжести человека \(Mg\), сила нормальной реакции \(N_1\) в точке A и сила реакции \(N_2\) в точке O. Так как лестница находится в равновесии, то запишем первое условие равновесия (первый закон Ньютона) в проекции на обе оси и второе условие равновесия (правило моментов) относительно точки O.
На лестницу действуют следующие силы: сила тяжести лестницы \(mg\), сила тяжести человека \(Mg\), сила нормальной реакции \(N_1\) в точке A и сила реакции \(N_2\) в точке O. Так как лестница находится в равновесии, то запишем первое условие равновесия (первый закон Ньютона) в проекции на обе оси и второе условие равновесия (правило моментов) относительно точки O.
\[\left\{ \begin{gathered}
{N_2} \cdot \sin \beta = mg + Mg \;\;\;\;(1)\hfill \\
{N_2} \cdot \cos \beta = {N_1} \;\;\;\;(2)\hfill \\
mg \cdot \frac{L}{2} \cdot \cos \alpha + Mg \cdot \left( {L — l} \right) \cdot \cos \alpha — {N_1} \cdot L \cdot \sin \alpha = 0 \;\;\;\;(3)\hfill \\
\end{gathered} \right.\]
Поделим равенства (1) и (2) друг на друга:
\[tg\beta = \frac{{\left( {m + M} \right)g}}{{{N_1}}}\;\;\;\;(4)\]
Из равенства (3) выразим реакцию \(N_1\):
\[{N_1} = \frac{{mgL \cdot \cos \alpha + 2Mg \cdot \left( {L — l} \right) \cdot \cos \alpha }}{{2L \cdot \sin \alpha }}\]
\[{N_1} = \frac{{\left( {mL + 2M\left( {L — l} \right)} \right)g}}{{2L \cdot tg\alpha }}\]
Полученное подставим в (4), тогда:
\[tg\beta = \frac{{\left( {m + M} \right)g \cdot 2L \cdot tg\alpha }}{{\left( {mL + 2M\left( {L — l} \right)} \right)g}}\]
\[tg\beta = \frac{{\left( {m + M} \right) \cdot 2L \cdot tg\alpha }}{{mL + 2M\left( {L — l} \right)}}\]
Окончательная формула примет вид:
\[\beta = arctg\left( {\frac{{\left( {m + M} \right) \cdot 2L \cdot tg\alpha }}{{mL + 2M\left( {L — l} \right)}}} \right)\]
Посчитаем численное значение искомого угла \(\beta\):
\[\beta = arctg\left( {\frac{{\left( {15 + 60} \right) \cdot 2 \cdot 3 \cdot tg60^\circ }}{{15 \cdot 3 + 2 \cdot 60 \cdot \left( {3 — 1} \right)}}} \right) = 70^\circ = 1,22\;рад\]
Ответ: 1,22 рад.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.1.21 К стене приставлена лестница массой 60 кг. Центр тяжести лестницы находится
3.1.23 Подъемное устройство состоит из однородного стержня длиной L=2,5 м и массой m=5 кг
3.1.24 Лестница составляет с землей угол 70 градусов и опирается о вертикальную гладкую
первое условие равновесия (первый закон Ньютона
Источник: https://easyfizika.ru/zadachi/statika/lestnitsa-massoj-15-kg-i-dlinoj-3-m-stoit-upirayas-verhnim-kontsom-v-gladkuyu-stenu
Исправьте, пожалуйста: Второй закон Ньютона
объясните, пожалуйста, почему если в системе отсчета N1 лежит на оси, в третьем уравнении вы умножили его на синус альфа?
а, все, понял
вопрос исчерпан
Почему не учитывается сила реакции опоры со стороны лестницы на человека?
Вы, задавая вопрос, уже ответили на него — эта сила действует на человека, а в уравнениях мы учитываем лишь силы, которые действуют на лестницу.
Силу, которая действует со стороны человека на лестницу, мы учли — это сила тяжести человека \(mg\).
Почему? Ведь человек не является частью лестницы. со стороны лестницу на человека действует сила реакции опоры N, направленная перпендикулярно лестнице, а в ответ по третьему закону Ньютона, на лестницу действует сила реакции N’, направленная вниз и перпендикулярно лестнице. Mg — это сила, действующая на человека, разве нет? И можете ещё объяснить, почему сила реакции опоры в нижней точке не перпендикулярно поверхности на которой она стоит?
Я так подозреваю, что так было, если бы не было человека? А человек за счёт своего веса прогибает лестницу, и поэтому сила реакции опоры стремится уменьшиться?
Нет, человек тут не при чем. Вообще, во всех задачах школьной статики конструкции (лестница в данном случае) недеформируемые, абсолютно жесткие, если в условии не сказано иного.
В общем случае реакция опоры имеет 2 взаимно перпендикулярны составляющие: нормальную (это та самая N) и касательную (сила трения). Если силы трения нет, то реакция перпендикулярна опоре (например, стене).
Почему сила реакции опоры со стороны боковой стены направлена перпендикулярно стене, а в случае пола не направлена перпендикулярно поверхности пола?
Потому что по условию стена — гладкая, то есть силы трения между верхним концом лестницы и стеной нету, а значит полная реакция направлена перпендикулярно стене.
А вот пол гладким быть не может, там обязательно должна быть сила трения покоя, которая уравновешивает реакцию N1. Поэтому полная реакция (которая есть векторная сумма нормальной и касательной, то есть силы трения) направлена под каким-то углом к вертикали.
Почему ответ в радианах ? И разве 60 градусов не будут ответом ?
Ответ переведен в радианы для самопроверки, т.к. ответ данной задачи в конце указанного сборника приведен в радианах.
Правильный ответ — 70°
По поводу законов Ньютона. Капиталисты, как я заметил, вообще не очень этим заморачиваются. Они говорят, что существует некая сила инерции равная m*a, а затем гребут всё под первый закон, то есть пишут для любой ситуации уравнение равновесия, но с учётом этой «силы инерции». Просто если тело движется равномерно и прямолинейно, эта сила равна нулю, а если с ускорением то нет.
Не знаю как там у капиталистов, но такой подход мне совсем не нравится. Меня учили прикладывать силу инерции для того, чтобы привести неинерциальную систему отсчета к инерциальной.
Зачем им вообще тогда второй закон Ньютона? Да и смысл первого в таком случае искажен.
Хотя такой подход хорошо использовать, например, чтобы объяснить соскальзывание тела с вращающегося диска без упоминания неинерциальной СО, связанной с диском.
Я бы заметил, что поскольку про силу N_1 нас никто не спрашивал, то и не стоит плодить лишние уравнения. Надо выбирать системы отсчёта, оси вращения удобные для решения конкретной задачи. В данном случае оставить уравнение (1), а уравнение моментов взять относительно точки O. И решать систему двух уравнений с двумя неизвестными, куда N_1 просто не вошло.
С одной стороны две проекции сил на оси и уравнение моментов универсально, с другой есть сложившаяся практика «убивать» лишние реакции правильным выбором оси вращения.
Вы, наверное, имели ввиду уравнение моментов взять относительно точки A — тогда я с Вами согласен.
Да, вы правы. Относительно точки О — это уже записанное уравнение (3).
Так как лестница находится в равновесии, то запишем первое условие равновесия (первый закон Ньютона) -вероятно запишем второй закон Ньютона
Почему? Лестница же стоит, то есть покоится. Для равновесия используем первый закон Ньютона.
А может быть третий закон Ньютона? — каждому действию своё противодействие (тела действуют друг на друга с силами равными по величине, противоположными по направлению, одной природы)
Нет, первое условие равновесия — это первый закон Ньютона, записанный в проекциях на две оси