Условие задачи:
К стене приставлена лестница массой 60 кг. Центр тяжести лестницы находится на расстоянии 1/3 длины от её верхнего конца. Какую горизонтальную силу нужно приложить к середине лестницы, чтобы её верхний конец не оказывал давления на стенку? Угол между лестницей и стеной равен 45°.
Задача №3.1.21 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=60\) кг, \(l=\frac{L}{3}\), \(\alpha=45^\circ\), \(F-?\)
Решение задачи:
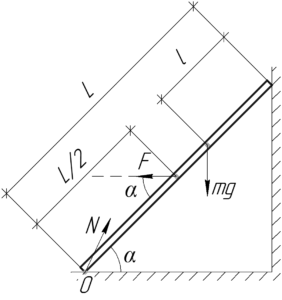Если верхний конец не будет оказывать давления на стенку, то на этот конец не будут действовать никакие силы со стороны стенки (ни сила нормальной реакции, ни сила трения). Тогда на лестницу действуют лишь три силы: сила тяжести \(mg\), сила реакции \(N\) в точке O и горизонтальная сила \(F\).
Лестница находится в равновесии. Запишем правило моментов (второе условие равновесия) относительно точки O – в этом случае момент силы реакции \(N\) равен нулю, так как равно нулю её плечо.
\[F \cdot \frac{L}{2} \cdot \sin \alpha – mg \cdot \left( {L – l} \right) \cdot \cos \alpha = 0\]
Так как по условию \(l=\frac{L}{3}\), то:
\[F \cdot \frac{L}{2} \cdot \sin \alpha – mg \cdot \left( {L – \frac{L}{3}} \right) \cdot \cos \alpha = 0\]
\[\frac{F}{2} \cdot \sin \alpha = \frac{{2mg}}{3} \cdot \cos \alpha \]
\[F = \frac{{4mg}}{3} \cdot ctg\alpha \]
Посчитаем ответ к задаче:
\[F = \frac{{4 \cdot 60 \cdot 10}}{3} \cdot ctg45^\circ = 800\;Н = 0,8\;кН\]
Ответ: 0,8 кН.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.1.20 Каков должен быть коэффициент трения, чтобы заколоченный в бревно клин
3.1.22 Лестница массой 15 кг и длиной 3 м стоит, упираясь верхним концом в гладкую стену
3.1.23 Подъемное устройство состоит из однородного стержня длиной L=2,5 м и массой m=5 кг
Почему мы пишем mg cos a, а не просто mg
Потому что относительно точки O плечо силы тяжести \(mg\) равно \(\left( {L – l} \right) \cdot \cos \alpha \)
Разве не должна быть еще сила терния?
Она есть, просто вместо того, чтобы в точке O изображать нормальную силу реакции и силу трения, я заменил их одной силой \(N\), которая является геометрической их суммой.
Как видно на рисунке, сила \(N\) (в данном случае это полная реакция) направлена под некоторым острым углом к полу (а не перпендикулярна ему). Если Вы спроецируете её на ось \(x\), то получите силу трения.
А если бы спрашивалось давление допустим в 1 Ньютон, верхнего конца, то нам бы еще нужно было записать момент для верхнего конца?
Да, Вам нужно было бы учесть ещё момент этой силы давления.
Почему F*L\2 на синус-то?
Потому что плечо указанной силы F есть противолежащий углу α катет в прямоугольном треугольнике, в котором гипотенуза равна L/2.