Условие задачи:
Взаимно перпендикулярные лучи идут из воздуха в жидкость. Каков показатель преломления жидкости, если один луч преломляется под углом 36°, а другой – под углом 20°?
Задача №10.3.11 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\gamma=90^\circ\), \(\beta_1=36^\circ\), \(\beta_2=20^\circ\), \(n_2-?\)
Решение задачи:
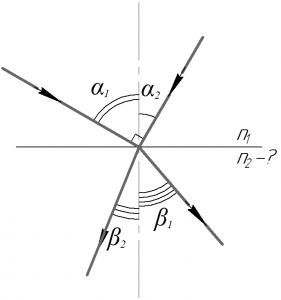Если угол падения одного из лучей к нормали к поверхности жидкости равен \(\alpha_1\), а угол между лучами равен \(\gamma\), то очевидно, что угол падения второго луча \(\alpha_2\) равен:
\[{\alpha _2} = {\gamma} – {\alpha _1}\]
Учитывая, что \(\gamma=90^\circ\), имеем (данная подстановка понадобится нам в дальнейшем):
\[{\alpha _2} = {90^\circ} – {\alpha _1}\;\;\;\;(1)\]
Запишем закон преломления света (также известен как закон преломления Снеллиуса) для обоих лучей:
\[\left\{ \begin{gathered}
{n_1}\sin {\alpha _1} = {n_2}\sin {\beta _1} \hfill \\
{n_1}\sin {\alpha _2} = {n_2}\sin {\beta _2} \hfill \\
\end{gathered} \right.\]
Здесь \(\alpha_1\) и \(\alpha_2\) – углы падения первого и второго луча, \(\beta_1\) и \(\beta_2\) – углы преломления первого и второго луча, \(n_1\) и \(n_2\) – показатели преломления сред. Показатель преломления воздуха \(n_1\) равен 1.
Учитывая формулу (1), имеем:
\[\left\{ \begin{gathered}
{n_1}\sin {\alpha _1} = {n_2}\sin {\beta _1} \hfill \\
{n_1}\sin \left( {{90^\circ} – {\alpha _1}} \right) = {n_2}\sin {\beta _2} \hfill \\
\end{gathered} \right.\]
Так как \(\sin \left( {90^\circ – {\alpha _1}} \right) = \cos {\alpha _1}\), то имеем:
\[\left\{ \begin{gathered}
{n_1}\sin {\alpha _1} = {n_2}\sin {\beta _1} \hfill \\
{n_1}\cos {\alpha _1} = {n_2}\sin {\beta _2} \hfill \\
\end{gathered} \right.\]
Сначала выразим из верхней формулы искомый показатель преломления жидкости \(n_2\):
\[{n_2} = \frac{{{n_1}}}{{\sin {\beta _1}}}\sin {\alpha _1}\;\;\;\;(2)\]
Чтобы найти \(\sin {\alpha _1}\), поделим нижнее уравнение системы на верхнее:
\[ctg{\alpha _1} = \frac{{\sin {\beta _2}}}{{\sin {\beta _1}}}\;\;\;\;(3)\]
Из тригонометрии известно следующее равенство:
\[1 + ct{g^2}{\alpha _1} = \frac{1}{{{{\sin }^2}{\alpha _1}}}\]
Откуда можно выразить \(\sin {\alpha _1}\) (отрицательный корень здесь опущен):
\[\sin {\alpha _1} = \sqrt {\frac{1}{{1 + ct{g^2}{\alpha _1}}}} \]
Учитывая (3), имеем:
\[\sin {\alpha _1} = \sqrt {\frac{1}{{1 + \frac{{{{\sin }^2}{\beta _2}}}{{{{\sin }^2}{\beta _1}}}}}} \]
\[\sin {\alpha _1} = \sqrt {\frac{{{{\sin }^2}{\beta _1}}}{{{{\sin }^2}{\beta _1} + {{\sin }^2}{\beta _2}}}} \]
\[\sin {\alpha _1} = \sin {\beta _1}\sqrt {\frac{1}{{{{\sin }^2}{\beta _1} + {{\sin }^2}{\beta _2}}}} \]
Осталось только полученное выражение подставить в формулу (2):
\[{n_2} = \frac{{{n_1}}}{{\sin {\beta _1}}}\sin {\beta _1}\sqrt {\frac{1}{{{{\sin }^2}{\beta _1} + {{\sin }^2}{\beta _2}}}} \]
\[{n_2} = {n_1}\sqrt {\frac{1}{{{{\sin }^2}{\beta _1} + {{\sin }^2}{\beta _2}}}} \]
Численный ответ равен:
\[{n_2} = 1 \cdot \sqrt {\frac{1}{{{{\sin }^2}36^\circ + {{\sin }^2}20^\circ }}} = 1,47\]
Ответ: 1,47.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.3.10 Водолазу, находящемуся под водой, кажется, что солнечные лучи падают под углом 60
10.3.12 Палка с изломом посередине погружена в пруд так, что наблюдателю, находящемуся
10.3.13 Под каким углом должен падать луч на поверхность стекла, чтобы угол преломления был