Условие задачи:

Угол падения луча на пластинку толщиной 6 мм и показателем преломления, равным \(\sqrt{3}\), равен углу полного внутреннего отражения для стекла, из которого изготовлена пластинка. Вычислить смещение луча при прохождении сквозь пластинку.

Задача №10.3.44 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=\alpha_{пр}\), \(d=6\) мм, \(n=\sqrt{3}\), \(l-?\)

Решение задачи:

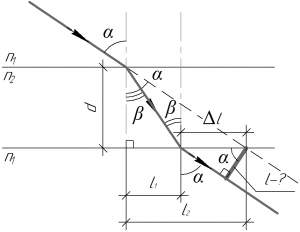Разумеется к такой задаче необходимо сделать хороший рисунок, без него решить задачу невозможно. Первое, что можно увидеть на рисунке, так это то, что искомое смещение \(l\) можно найти из прямоугольного треугольника по формуле:

\[l = \Delta l\cos \alpha\;\;\;\;(1)\]

Расстояние \(\Delta l\) можно определить следующим образом:

\[\Delta l = {l_2} — {l_1}\]

Расстояния \(l_1\) и \(l_2\) можно найти из соответствующих прямоугольных треугольников (да, опять) по следующим формулам:

\[\left\{ \begin{gathered}
{l_2} = d \cdot tg\alpha \hfill \\
{l_1} = d \cdot tg\beta \hfill \\
\end{gathered} \right.\]

Учитывая все вышесказанное, формула (1) примет вид:

\[l = d\cos \alpha \left( {tg\alpha — tg\beta } \right)\;\;\;\;(2)\]

Чтобы найти угол падения \(\alpha\), запишем закон преломления света (также известен как закон преломления Снеллиуса) для случая полного внутреннего отражения для стекла, из которого изготовлена пластинка, при переходе в воздух:

\[n \sin \alpha_{пр} = {n_0}\]

Здесь \(\alpha_{пр}\) — угол полного внутреннего отражения при падении на границу стекло-воздух, \(n\) и \(n_0\) — показатели преломления сред. Показатель преломления воздуха \(n_0\) равен 1. Тогда:

\[\sin {\alpha _{пр}} = \frac{{{n_0}}}{n}\;\;\;\;(3)\]

\[{\alpha _{пр}} = \arcsin \left( {\frac{{{n_0}}}{n}} \right)\]

По условию угол падения луча на пластинку равен углу полного внутреннего отражения для стекла, из которого изготовлена пластинка, то есть \(\alpha = \alpha_{пр}\), поэтому:

\[\alpha = \arcsin \left( {\frac{{{n_0}}}{n}} \right)\;\;\;\;(4)\]

Чтобы найти угол преломления \(\beta\), запишем закон преломления света (также известен как закон преломления Снеллиуса) при переходе из воздуха в стекло:

\[{n_0}\sin \alpha = n\sin \beta\]

Имеем:

\[\sin \alpha = \frac{{n\sin \beta }}{{{n_0}}}\;\;\;\;(5)\]

Так как \(\alpha = \alpha_{пр}\), приравняем (3) и (4):

\[\frac{{{n_0}}}{n} = \frac{{n\sin \beta }}{{{n_0}}}\]

\[\sin \beta = \frac{{n_0^2}}{{{n^2}}}\]

То есть:

\[\beta = \arcsin \left( {\frac{{n_0^2}}{{{n^2}}}} \right)\;\;\;\;(6)\]

Осталось только подставить выражения (4) и (6) в формулу (2):

\[l = d\cos \left( {\arcsin \left( {\frac{{{n_0}}}{n}} \right)} \right)\left( {tg\left( {\arcsin \left( {\frac{{{n_0}}}{n}} \right)} \right) — tg\left( {\arcsin \left( {\frac{{n_0^2}}{{{n^2}}}} \right)} \right)} \right)\]

Задача решена в общем виде, подставим данные задачи в полученную формулу и посчитаем численный ответ:

\[l = 0,006 \cdot \cos \left( {\arcsin \left( {\frac{1}{{\sqrt 3 }}} \right)} \right)\left( {tg\left( {\arcsin \left( {\frac{1}{{\sqrt 3 }}} \right)} \right) — tg\left( {\arcsin \left( {\frac{1}{3}} \right)} \right)} \right) = 1,732 \cdot {10^{ — 3}}\;м = 0,17\;cм\]

Ответ: 0,17 cм.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.