Решение: Светящаяся точка приближается к собирающей линзе вдоль ее главной оптической оси

Условие задачи:

Светящаяся точка приближается к собирающей линзе вдоль ее главной оптической оси с постоянной скоростью 2 см/с. Какова средняя скорость движения изображения точки на участке пути между двумя его положениями, удаленными от линзы на расстояния, равные двум и четырем фокусным расстояниям линзы?

Задача №10.5.70 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon=2\) см/с, \(f_1=2F\), \(f_2=4F\), \(u_{ср}-?\)

Решение задачи:

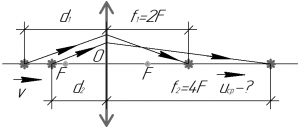Очевидно, что среднюю скорость движения изображения светящейся точки можно определить по следующей довольно простой формуле:

\[{u_{ср}} = \frac{{{f_2} — {f_1}}}{t}\]

Так как по условию задачи \(f_1=2F\) и \(f_2=4F\), то:

\[{u_{ср}} = \frac{{4F — 2F}}{t}\]

\[{u_{ср}} = \frac{{2F}}{t}\;\;\;\;(1)\]

Чтобы получить ответ на вопрос задачи, нам нужно найти время \(t\), за которое изображение светящейся точки прошло путь \(2F\). Как это можно сделать? В данном случае мы можем это сделать через движение самой движущейся точки, ведь мы можем определить, где находится точка, когда её изображение находится на расстояниях \(f_1\) и \(f_2\), а также мы знаем скорость движения точки \(\upsilon\):

\[t = \frac{{{d_1} — {d_2}}}{\upsilon }\;\;\;\;(2)\]

Запишем формулу тонкой линзы:

\[\frac{1}{F} = \frac{1}{d} + \frac{1}{f}\;\;\;\;(3)\]

В этой формуле \(F\) — фокусное расстояние линзы, знак перед ним «+», поскольку линза — собирающая, \(d\) — расстояние от линзы до предмета, знак перед ним «+», поскольку предмет — действительный (в случае одиночной линзы предмет всегда действительный, оно бывает мнимым в случае системы линз), \(f\) — расстояние от линзы до изображения, знак перед ним «+», поскольку изображение — действительное (то есть образуется на сходящемся пучке лучей — смотрите рисунок).

Тогда из формулы (3) выразим неизвестное расстояние от линзы до изображения \(d\):

\[\frac{1}{d} = \frac{1}{F} — \frac{1}{f}\]

\[\frac{1}{d} = \frac{{f — F}}{{Ff}}\]

\[d = \frac{{fF}}{{f — F}}\]

Запишем полученную формулу для определения расстояний \(d_1\) и \(d_2\):

\[\left\{ \begin{gathered}
{d_1} = \frac{{{f_1}F}}{{{f_1} — F}} \hfill \\
{d_2} = \frac{{{f_2}F}}{{{f_2} — F}} \hfill \\
\end{gathered} \right.\]

Опять вспоминаем, что по условию задачи \(f_1=2F\) и \(f_2=4F\), поэтому:

\[\left\{ \begin{gathered}
{d_1} = \frac{{2F \cdot F}}{{2F — F}} \hfill \\
{d_2} = \frac{{4F \cdot F}}{{4F — F}} \hfill \\
\end{gathered} \right.\]

\[\left\{ \begin{gathered}
{d_1} = 2F \hfill \\
{d_2} = \frac{{4F}}{3} \hfill \\
\end{gathered} \right.\]

С учетом полученного формула (2) примет вид:

\[t = \frac{{2F — \frac{{4F}}{3}}}{\upsilon }\]

\[t = \frac{{2F}}{{3\upsilon }}\]