Решение: Сечение стеклянной призмы имеет вид равностороннего треугольника. Луч света падает

Условие задачи:

Сечение стеклянной призмы имеет вид равностороннего треугольника. Луч света падает из воздуха на одну из граней призмы перпендикулярно ей. Найти угол преломления луча при выходе из призмы. Показатель преломления стекла равен 1,5.

Задача №10.3.37 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(n_1=1,5\), \(\gamma-?\)

Решение задачи:

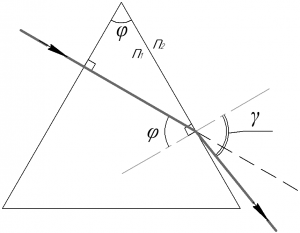Сделаем к этой задаче рисунок, без него решить задачу невозможно. Так как призма имеет вид равностороннего треугольника, то угол \(\varphi\) равен 60°.

Известно, что если луч падает перпендикулярно на грань прозрачной призмы, то он не преломляется, поэтому преломлять луч будет только вторая грань. На нее луч будет падать под углом \(\varphi\) к нормали, это видно из рисунка (см. на прямые углы).

Чтобы найти искомый угол преломления \(\gamma\), запишем закон преломления света (также известен как закон преломления Снеллиуса):

\[{n_1}\sin \varphi = {n_2}\sin \gamma\]

Здесь \(\varphi\) и \(\gamma\) — угол падения и угол преломления соответственно, \(n_1\) и \(n_2\) — показатели преломления сред. Показатель преломления воздуха \(n_2\) равен 1.

Тогда:

\[\sin \gamma = \frac{{{n_1}\sin \varphi }}{{{n_2}}}\]

\[\gamma = \arcsin \left( {\frac{{{n_1}\sin \varphi }}{{{n_2}}}} \right)\]

Задача решена в общем виде, подставим данные задачи в полученную формулу и посчитаем численный ответ:

\[\gamma = \arcsin \left( {\frac{{1,5 \cdot \sin 60^\circ }}{1}} \right)\]

При расчете на калькуляторе вы должны получить ошибку. Если разбираться почему, то станет понятно, что аргумент арксинуса не должен быть больше единицы. Это наталкивает нас на мысль, что здесь наблюдается явление полного внутреннего отражения. Давайте найдем предельный угол полного отражения \(\varphi_{пр}\):

\[{\varphi _{пр}} = \arcsin \left( {\frac{{{n_2}}}{{{n_1}}}} \right)\]

\[{\varphi _{пр}} = \arcsin \left( {\frac{1}{{1,5}}} \right) = 41,8^\circ \]

Так как угол падения луча на вторую грань \(\varphi\) больше, чем предельный угол полного отражения \(\varphi_{пр}\), значит луч из призмы не выйдет.