Условие задачи:
Расстояние от предмета до линзы и от линзы до изображения предмета одинаковы и равны 60 см. Во сколько раз увеличится изображение, если предмет поместить на 20 см ближе к линзе?
Задача №10.5.55 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(d=f=60\) см, \(\Delta d =20\) см, \(\frac{H_2}{H_1}-?\)
Решение задачи:
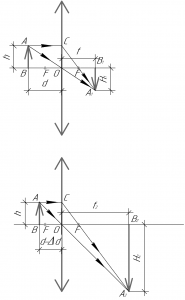Мы имеем дело с собирающей линзой, поскольку рассеивающая линза не может давать действительного изображения.
Покажем общий принцип построения изображения в собирающей линзе. Чтобы построить изображение точки A в собирающей линзе в данном случае, нужно провести через точку A два луча: один параллельно главной оптической оси, а второй через главный оптический центр O. Первый луч, преломившись в линзе, пройдет через задний фокус линзы. Второй луч проходит через линзу, не преломляясь. На пересечении этих лучей и будет находиться точка A1. Проекция этой точки на главную оптическую ось есть точка B1. Вот и все, изображение построено. Как мы видим, оно получилось действительным (поскольку получается на сходящемся пучке лучей) и перевернутым.
Запишем формулу тонкой линзы для собирающей линзы для первого случая, когда линза дает действительное изображение:
\[\frac{1}{F} = \frac{1}{d} + \frac{1}{f}\]
В этой формуле \(F\) — фокусное расстояние линзы, знак перед ним «+», поскольку линза — собирающая, \(d\) — расстояние от линзы до предмета, знак перед ним «+», поскольку предмет — действительный (в случае одиночной линзы предмет всегда действительный, оно бывает мнимым в случае системы линз), \(f\) — расстояние от линзы до изображения, знак перед ним «+», поскольку изображение — действительное (то есть образуется на сходящемся пучке лучей — смотрите рисунок).
Так как по условию \(d=f\), то имеем:
\[\frac{1}{F} = \frac{2}{d}\;\;\;\;(1)\]
Также из подобия треугольников AOB и A1OB1 запишем следующее равенство:
\[\frac{f}{d} = \frac{{{H_1}}}{h}\]
Опять, так как по условию \(d=f\), то имеем:
\[{H_1} = h\;\;\;\;(2)\]
Запишем формулу тонкой линзы для второго случая после перемещения предмета к линзе:
\[\frac{1}{F} = \frac{1}{{d — \Delta d}} + \frac{1}{{{f_2}}}\]
Учитывая (1), имеем:
\[\frac{2}{d} = \frac{1}{{d — \Delta d}} + \frac{1}{{{f_2}}}\]
\[\frac{2}{d} — \frac{1}{{d — \Delta d}} = \frac{1}{{{f_2}}}\]
\[\frac{{2d — 2\Delta d — d}}{{d\left( {d — \Delta d} \right)}} = \frac{1}{{{f_2}}}\]
\[\frac{{d — 2\Delta d}}{{d\left( {d — \Delta d} \right)}} = \frac{1}{{{f_2}}}\]
В итоге мы найдем неизвестное расстояние от линзы до изображения \(f_2\):
\[{f_2} = \frac{{d\left( {d — \Delta d} \right)}}{{d — 2\Delta d}}\;\;\;\;(3)\]
Аналогично, из подобия треугольников AOB и A2OB2 запишем следующее равенство:
\[\frac{{{H_2}}}{h} = \frac{{{f_2}}}{{d — \Delta d}}\]
Учитывая ранее полученное равенство (2), имеем:
\[\frac{{{H_2}}}{{{H_1}}} = \frac{{{f_2}}}{{d — \Delta d}}\]
А если учесть выражение (3), окончательно получим:
\[\frac{{{H_2}}}{{{H_1}}} = \frac{d}{{d — 2\Delta d}}\]
Посчитаем численный ответ задачи:
\[\frac{{{H_2}}}{{{H_1}}} = \frac{{0,6}}{{0,6 — 2 \cdot 0,2}} = 3\]
Ответ: в 3 раза.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.5.54 Собирающая линза дает двукратное изображение предмета. Когда линзу придвинули
10.5.56 От предмета высотой 20 см при помощи линзы получили действительное изображение
10.5.57 Предмет расположен перпендикулярно оптической оси собирающей линзы. На сколько