Условие задачи:

Расстояние между предметом и его равным, действительным изображением равно 2 м. Определить оптическую силу линзы.

Задача №10.5.33 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\Gamma = 1\), \(z=2\) м, \(D-?\)

Решение задачи:

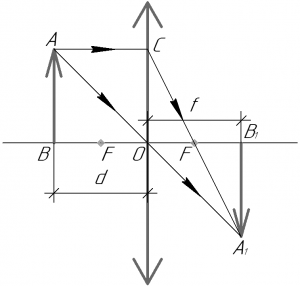В задаче мы имеем дело с собирающей линзой, так как только с помощью такой линзы можно получить действительное изображение. При этом предмет должен находится левее переднего фокуса линзы, то есть \({d} > {F}\).

Чтобы построить изображение точки A в собирающей линзе, нужно провести через точку A два луча: один параллельно главной оптической оси, а второй через главный оптический центр O. Первый луч, преломившись в линзе в точке C, пройдет через задний фокус линзы. Второй луч проходит через линзу, не преломляясь. На пересечении этих лучей и будет находиться точка A₁. Проекция этой точки на главную оптическую ось есть точка B₁. Вот и все, изображение построено. Как мы видим, оно получилось действительным (поскольку получается на сходящемся пучке лучей) и перевернутым.

Запишем формулу тонкой линзы для этого случая:

\[D = \frac{1}{d} + \frac{1}{f}\]

В этой формуле \(D\) — оптическая сила линзы, это положительная величина, поскольку линза — собирающая, \(d\) — расстояние от линзы до предмета, знак перед ним «+», поскольку предмет — действительный (в случае одиночной линзы предмет всегда действительный, оно бывает мнимым в случае системы линз), \(f\) — расстояние от линзы до изображения, знак перед ним «+», поскольку изображение — действительное (то есть образуется на сходящемся пучке лучей — смотрите рисунок).

Приведем уравнение под общий знаменатель:

\[D = \frac{{d + f}}{{df}}\;\;\;\;(1)\]

Поперечное увеличение предмета в линзе \(\Gamma\) определяют по формуле (это можно вывести из подобия треугольников AOB и A₁OB₁):

\[\Gamma = \frac{f}{d}\]

Тогда:

\[f = \Gamma d\;\;\;\;(2)\]

Тогда уравнение (1) примет вид:

\[D = \frac{{d + \Gamma d}}{{\Gamma {d^2}}}\]

\[D = \frac{{\Gamma + 1}}{{\Gamma d}}\;\;\;\;(3)\]

Из рисунка видно, что данное в условии расстояние между предметом и экраном (изображением) \(z\) можно выразить следующим образом:

\[z = d + f\;\;\;\;(4)\]

Учитывая (2), формулу (4) можно записать в виде:

\[z = d + \Gamma d\]

\[z = d\left( {\Gamma + 1} \right)\]

Откуда выразим расстояние от линзы до предмета \(d\):

\[d = \frac{z}{{\Gamma + 1}}\;\;\;\;(5)\]

Подставим выражение (5) в уравнение (3):

\[D = \frac{{\Gamma + 1}}{\Gamma } \cdot \frac{{\Gamma + 1}}{z}\]

Окончательно получим такое решение этой задачи в общем виде:

\[D = \frac{{{{\left( {\Gamma + 1} \right)}^2}}}{{\Gamma z}}\]

Посчитаем численный ответ задачи:

\[D = \frac{{{{\left( {1 + 1} \right)}^2}}}{{1 \cdot 2}} = 2\;дптр\]

Ответ: 2 дптр.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

10.5.32 Найти наименьшее возможное расстояние между светящимся предметом и его
10.5.34 С помощью линзы на экране получено изображение в 4 раза по площади больше самого
10.5.35 Перед собирающей линзой с оптической силой 2,5 дптр на расстоянии 30 см находится