Решение: Предмет расположен на расстоянии 1,6F от линзы. Его переместили к линзе на расстояние

Условие задачи:

Предмет расположен на расстоянии 1,6F от линзы. Его переместили к линзе на расстояние 0,8F. Насколько при этом переместилось изображение предмета, если оптическая сила линзы 2,5 дптр? F – фокусное расстояние линзы.

Задача №10.5.52 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(d_1=1,6F\), \(d_2=0,8F\), \(D=2,5\) дптр, \(\Delta f-?\)

Решение задачи:

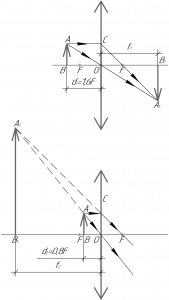В данном случае мы имеем дело с собирающей линзой, поскольку её оптическая сила положительная.

Нам нужно построить изображение предмета для двух разных случаев (при различном расстоянии от предмета до линзы \(d\)). Интересно, что в первом случае линза будет давать действительное изображение предмета (поскольку \({d} > {F}\)), а во втором случае – мнимое (так как в этом случае \({d} < {F}\)). Более подробно Вы можете все посмотреть на рисунках.

Рассмотрим первый случай. Чтобы построить изображение точки A в собирающей линзе в данном случае, нужно провести через точку A два луча: один параллельно главной оптической оси, а второй через главный оптический центр O. Первый луч, преломившись в линзе в точке C, пройдет через задний фокус линзы. Второй луч проходит через линзу, не преломляясь. На пересечении этих лучей и будет находиться точка A₁. Проекция этой точки на главную оптическую ось есть точка B₁. Вот и все, изображение построено. Как мы видим, оно получилось действительным (поскольку получается на сходящемся пучке лучей) и перевернутым.

Запишем формулу тонкой линзы для этого случая:

\[\frac{1}{F} = \frac{1}{{{d_1}}} + \frac{1}{{{f_1}}}\;\;\;\;(1)\]

В этой формуле \(F\) – фокусное расстояние линзы, знак перед ним “+”, поскольку линза – собирающая, \(d_1\) – расстояние от линзы до предмета, знак перед ним “+”, поскольку предмет – действительный (в случае одиночной линзы предмет всегда действительный, оно бывает мнимым в случае системы линз), \(f_1\) – расстояние от линзы до изображения, знак перед ним “+”, поскольку изображение – действительное (то есть образуется на сходящемся пучке лучей – смотрите рисунок).

Из формулы (1) имеем:

\[\frac{1}{{{f_1}}} = \frac{1}{F} – \frac{1}{{{d_1}}}\]

В правой части полученного уравнения приведем под общий знаменатель:

\[\frac{1}{{{f_1}}} = \frac{{{d_1} – F}}{{{d_1}F}}\]

\[{f_1} = \frac{{{d_1}F}}{{{d_1} – F}}\]

По условию задачи \(d_1=1,6F\), поэтому:

\[{f_1} = \frac{{1,6F \cdot F}}{{1,6F – F}} = \frac{8}{3}F\;\;\;\;(2)\]

Перейдем ко второму случаю. Чтобы построить изображение точки A в собирающей линзе, нужно провести через точку A два луча: один параллельно главной оптической оси, а второй через главный оптический центр O. Первый луч, преломившись в линзе в точке C, пройдет через задний фокус линзы. Второй луч проходит через линзу, не преломляясь. Так как лучи не пересекаются, то их нужно продлить влево. На пересечении продолжений этих лучей и будет находиться точка A₁. Проекция этой точки на главную оптическую ось есть точка B₁. Вот и все, изображение построено. Как мы видим, оно получилось мнимым (поскольку получается на расходящемся пучке лучей), прямым и увеличенным (\(\Gamma > 1\)).

Запишем формулу тонкой линзы для этого случая:

\[\frac{1}{F} = \frac{1}{{{d_2}}} – \frac{1}{{{f_2}}}\;\;\;\;(3)\]

В этой формуле \(F\) – фокусное расстояние линзы, знак перед ним “+”, поскольку линза – собирающая, \(d_2\) – расстояние от линзы до предмета, знак перед ним “+”, поскольку предмет – действительный (в случае одиночной линзы предмет всегда действительный, оно бывает мнимым в случае системы линз), \(f_2\) – расстояние от линзы до изображения, знак перед ним “-“, поскольку изображение – мнимое (то есть образуется на расходящемся пучке лучей – смотрите рисунок).

Из формулы (3) выразим расстояние от линзы до изображения \(f_2\):

\[\frac{1}{{{f_2}}} = \frac{1}{{{d_2}}} – \frac{1}{F}\]

В правой части полученного уравнения приведем под общий знаменатель:

\[\frac{1}{{{f_2}}} = \frac{{F – {d_2}}}{{{d_2}F}}\]

\[{f_2} = \frac{{{d_2}F}}{{F – {d_2}}}\]

По условию задачи \(d_2=0,8F\), поэтому:

\[{f_2} = \frac{{0,8F \cdot F}}{{F – 0,8F}} = 4F\;\;\;\;(4)\]

Из приведенных рисунков прекрасно видно, что искомое расстояние \(\Delta f\), на которое переместилось изображение предмета легко найти по формуле:

\[\Delta f = {f_1} + {f_2}\]

Учитывая полученные ранее выражения (2) и (4), получим:

\[\Delta f = \frac{8}{3}F + 4F\]

\[\Delta f = \frac{{20}}{3}F\]