Решение: Предмет помещен между двумя взаимно перпендикулярными зеркалами. Сколько

Условие задачи:

Предмет помещен между двумя взаимно перпендикулярными зеркалами. Сколько получается изображения?

Задача №10.1.12 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=90^\circ\), \(N-?\)

Решение задачи:

Вообще, есть формула, которая позволяет рассчитать количество изображений, получающихся между двумя зеркалами, расположенными под углом \(\alpha\) друг к другу:

\[N = \frac{{360^\circ }}{\alpha } – 1\]

Применительно к нашей задаче, учитывая, что \(\alpha=90^\circ\):

\[N = \frac{{360^\circ }}{{90^\circ }} – 1 = 3\]

Интересно. Интуитивно кажется, что ответ должен быть 2, т.е. от каждого зеркала получится по одному изображению. Будем разбираться, в чем же тут дело.

Напомним, что изображение предмета в плоском зеркале симметрично самому предмету относительно плоскости зеркала. Поэтому для построения изображения предмета в плоском зеркале достаточно построить точки, симметричные точкам предмета.

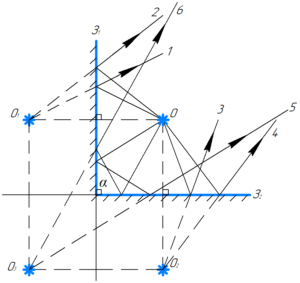
Исходя из этого, мы легко построили изображения O₁ и O₂ соответственно в зеркалах З₁ и З₂ (см. рисунок). Но откуда должно получиться изображение O₃?

Давайте вспомним, что такое изображение точки – это точка пересечения лучей (или их продолжений), прошедших через оптическую систему. Для построения изображения точки необходимо два луча. Изображение O₁ получается на пересечении продолжений лучей 1 и 2, которые отразились от зеркала З₁. Изображение O₂ получается на пересечении продолжений лучей 3 и 4, которые отразились от зеркала З₂. А вот изображение O₃ получается на пересечении продолжений лучей 5 и 6. Причем оба этих луча отразились от обоих зеркал!

Интересно, если мы продолжим зеркало З₁, то изображение O₃ – это изображение изображения O₂. Или если продолжить зеркало З₂, то изображение O₃ – это изображение изображения O₁.