Решение: Под каким углом должен падать луч света на плоскую поверхность льда, чтобы

Условие задачи:

Под каким углом должен падать луч света на плоскую поверхность льда, чтобы преломленный луч образовал прямой угол с отраженным лучом?

Задача №10.3.19 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\gamma = 90^\circ\), \(\alpha-?\)

Решение задачи:

Запишем закон преломления света (также известен как закон преломления Снеллиуса):

\[{n_1}\sin \alpha = {n_2}\sin \beta\;\;\;\;(1)\]

Здесь \(\alpha\) и \(\beta\) — угол падения и угол преломления соответственно, \(n_1\) и \(n_2\) — показатели преломления сред. Показатель преломления воздуха \(n_1\) равен 1, показатель преломления льда \(n_2\) равен 1,31.

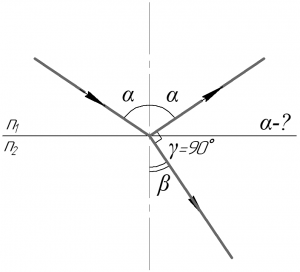
Так как по условию задачи преломленный луч образовывает прямой угол с отраженным лучом, то из рисунка хорошо видно, что сумма угла отражения и угла преломления также равна 90°, то есть:

\[\alpha + \beta = 90^\circ \]

\[\beta = 90^\circ — \alpha \]

Тогда уравнение (1) примет вид:

\[{n_1}\sin \alpha = {n_2}\sin \left( {90^\circ — \alpha } \right)\]

Известно, что \(\sin \left( {90^\circ — \alpha } \right) = \cos \alpha\), поэтому:

\[{n_1}\sin \alpha = {n_2}\cos \alpha \]

Перенесем все в левую часть:

\[{n_1}\sin \alpha — {n_2}\cos \alpha = 0\]

Выражения вида \(A\sin x — B\cos x\) приводятся к виду \(C\sin \left( {x — t} \right)\), где \(C = \sqrt {{A^2} + {B^2}}\) и \(t = arctg\frac{B}{A}\). Поэтому:

\[\sqrt {n_1^2 + n_2^2} \sin \left( {\alpha — arctg\frac{{{n_2}}}{{{n_1}}}} \right) = 0\]

Так как множитель перед синусом точно не равен нулю, имеем:

\[\sin \left( {\alpha — arctg\frac{{{n_2}}}{{{n_1}}}} \right) = 0\]

Синус равен нулю, когда его аргумент равен нулю:

\[\alpha — arctg\frac{{{n_2}}}{{{n_1}}} = 0\]

\[\alpha = arctg\frac{{{n_2}}}{{{n_1}}}\]

Задача решена в общем виде, подставим численные данные в полученную формулу и посчитаем численный ответ:

\[\alpha = arctg\frac{{1,31}}{1} = 52,6^\circ \]