Условие задачи:
Определите оптическую разность хода волн длиной 540 нм, падающих на дифракционную решетку нормально и образовавших максимум второго порядка.
Задача №10.7.25 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\lambda=540\) нм, \(k=2\), \(\Delta-?\)
Решение задачи:
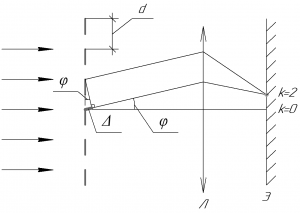Запишем формулу дифракционной решетки:
\[d\sin \varphi = k\lambda\;\;\;\;(1)\]
В этой формуле \(d\) – период решетки (также называют постоянной решетки), \(\varphi\) – угол дифракции, \(k\) – порядок максимума, \(\lambda\) – длина волны, падающей нормально на решетку.
Тем, кто знаком с выводом формулы дифракционной решетки, известно, что слева и справа от знака “равно” содержится та самая искомая разность хода \(\Delta\), поэтому:
\[\Delta = k\lambda \]
Посчитаем численный ответ:
\[\Delta = 2 \cdot 540 \cdot {10^{ – 9}} = 1,08 \cdot {10^{ – 6}}\;м = 1,08\;мкм\]
Ответ: 1,08 мкм.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.7.24 Период дифракционной решетки равен 1,5 мкм. Чему равна ширина прозрачных щелей
10.7.26 Дифракционная решетка, имеющая 100 штрихов на 1 мм, находится на расстоянии 1 м
10.7.27 На дифракционную решетку с периодом 4 мкм падает нормально монохроматическая волна