Решение: Определить угол отклонения луча призмой. Преломляющий угол призмы равен 60°

Условие задачи:

Определить угол отклонения луча призмой. Преломляющий угол призмы равен 60°. Угол падения луча на грань призмы равен 30°, а показатель преломления вещества призмы равен 1,5.

Задача №10.3.38 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\varphi=60^\circ\), \(\alpha=30^\circ\), \(n_1=1,5\), \(\theta-?\)

Решение задачи:

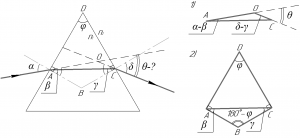Сделаем к этой задаче рисунок, без него решить задачу невозможно. В задаче очень много геометрии и практически нет физики. Итак, начнем.

Рассмотрим треугольник AOC (смотрите рисунок 1). Искомый угол \(\theta\) является смежным для этого треугольника, поэтому справедливо:

\[\theta = \left( {\alpha – \beta } \right) + \left( {\delta – \gamma } \right)\]

\[\theta = \alpha + \delta – \left( {\beta + \gamma } \right)\;\;\;\;(1)\]

Далее рассмотрим четырёхугольник ABCD (смотрите рисунок 2). В этом четырехугольнике два угла – прямые, поэтому угол ABC равен \(\left( {180^\circ – \varphi } \right)\). На этом рисунке теперь рассмотрим треугольник ABC. Сумма углов любого треугольника равна 180°, поэтому будет верно записать:

\[\beta + \gamma + \left( {180^\circ – \varphi } \right) = 180^\circ \]

\[\varphi = \beta + \gamma \;\;\;\;(2)\]

Тогда уравнение (1) примет вид:

\[\theta = \alpha + \delta – \varphi \;\;\;\;(3)\]

Чтобы найти угол преломления \(\delta\), запишем закон преломления света (также известен как закон преломления Снеллиуса):

\[{n_1}\sin \gamma = {n_2}\sin \delta \]

Здесь \(\gamma\) и \(\delta\) – угол падения и угол преломления соответственно, \(n_1\) и \(n_2\) – показатели преломления сред. Показатель преломления воздуха \(n_2\) равен 1. Тогда:

\[\sin \delta = \frac{{{n_1}\sin \gamma }}{{{n_2}}}\]

\[\delta = \arcsin \left( {\frac{{{n_1}}}{{{n_2}}}\sin \gamma } \right)\]

Из равенства (2) также следует, что \(\gamma = \varphi – \beta\), поэтому:

\[\delta = \arcsin \left( {\frac{{{n_1}}}{{{n_2}}}\sin \left( {\varphi – \beta } \right)} \right)\;\;\;\;(4)\]

Чтобы найти угол преломления \(\beta\), опять запишем закон преломления света:

\[{n_2}\sin \alpha = {n_1}\sin \beta \]

Здесь \(\alpha\) и \(\beta\) – угол падения и угол преломления соответственно, \(n_1\) и \(n_2\) – показатели преломления сред. Тогда:

\[\sin \beta = \frac{{{n_2}\sin \alpha }}{{{n_1}}}\]

\[\beta = \arcsin \left( {\frac{{{n_2}\sin \alpha }}{{{n_1}}}} \right)\]

Полученное выражение подставим в (4):

\[\theta = \alpha – \varphi + \arcsin \left( {\frac{{{n_1}}}{{{n_2}}}\sin \left( {\varphi – \arcsin \left( {\frac{{{n_2}\sin \alpha }}{{{n_1}}}} \right)} \right)} \right)\]

Задача решена в общем виде, подставим данные задачи в полученную формулу и посчитаем численный ответ:

\[\theta = 30^\circ – 60^\circ + \arcsin \left( {\frac{{1,5}}{1}\sin \left( {60^\circ – \arcsin \left( {\frac{{1 \cdot \sin 30^\circ }}{{1,5}}} \right)} \right)} \right) = 47,1^\circ \]