Решение: Определить наименьшее возможное расстояние между светящимся предметом и его

Условие задачи:

Определить наименьшее возможное расстояние между светящимся предметом и его действительным изображением в собирающей линзе с фокусным расстоянием 30 см.

Задача №10.5.28 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(F=30\) см, \(z_{\min}-?\)

Решение задачи:

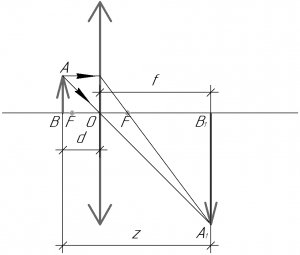Понятно, что предмет находится левее переднего фокуса линзы, то есть \({d} > {F}\).

Чтобы построить изображение точки A в собирающей линзе, нужно провести через точку A два луча: один параллельно главной оптической оси, а второй через главный оптический центр O. Первый луч, преломившись в линзе, пройдет через задний фокус линзы. Второй луч проходит через линзу, не преломляясь. На пересечении этих лучей и будет находиться точка A₁. Проекция этой точки на главную оптическую ось есть точка B₁. Вот и все, изображение построено. Как мы видим, оно получилось действительным (поскольку получается на сходящемся пучке лучей) и перевернутым.

Запишем формулу тонкой линзы:

\[\frac{1}{F} = \frac{1}{d} + \frac{1}{f}\;\;\;\;(1)\]

В этой формуле \(F\) – фокусное расстояние линзы, знак перед ним “+”, поскольку линза – собирающая, \(d\) – расстояние от линзы до предмета, знак перед ним “+”, поскольку предмет – действительный (в случае одиночной линзы предмет всегда действительный, оно бывает мнимым в случае системы линз), \(f\) – расстояние от линзы до изображения, знак перед ним “+”, поскольку изображение – действительное (то есть образуется на сходящемся пучке лучей – смотрите рисунок).

Из рисунка видно, что данное в условии расстояние между предметом и экраном (изображением) \(z\) можно выразить следующим образом:

\[z = d + f\]

Имеем:

\[f = z – d\;\;\;\;(2)\]

Тогда уравнение (1) с учетом выражения (2) примет вид:

\[\frac{1}{F} = \frac{1}{d} + \frac{1}{{z – d}}\]

Приведем правую часть уравнения под общий знаменатель:

\[\frac{1}{F} = \frac{{z – d + d}}{{d\left( {z – d} \right)}}\]

\[\frac{1}{F} = \frac{z}{{d\left( {z – d} \right)}}\]

Перемножим “крест-накрест”, раскроем скобки и перенесем все в одну сторону:

\[zF = d\left( {z – d} \right)\]

\[zF = dz – {d^2}\]

\[{d^2} – zd + zF = 0\]

Чтобы полученное квадратное уравнение относительно \(d\) имело хоть какой-нибудь корень, его дискриминант \(D_{диск}\) должен быть больше или равен нулю:

\[{D_{диск}} = {z^2} – 4zF\]

\[{z^2} – 4zF \geq 0\]

\[z\left( {z – 4F} \right) \geq 0\]

При решении мы получим следующую совокупность:

\[\left[ \begin{gathered}
z \leq 0 \hfill \\
z \geq 4F \hfill \\
\end{gathered} \right.\]

Понятно, что расстояние между предметом и линзой не может быть отрицательным, поэтому искомое минимальное расстояние между предметом и линзой \(z_{\min}\) равно:

\[{z_{\min }} = 4F\]

Посчитаем численный ответ задачи:

\[{z_{\min }} = 4 \cdot 0,3 = 1,2\;м\]