Решение: Определить на какой угол отклоняется узкий световой пучок от своего первоначального

Условие задачи:

Определить на какой угол отклоняется узкий световой пучок от своего первоначального положения при переходе из стекла в воздух, если угол падения 30°.

Задача №10.3.16 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=30^\circ\), \(\gamma-?\)

Решение задачи:

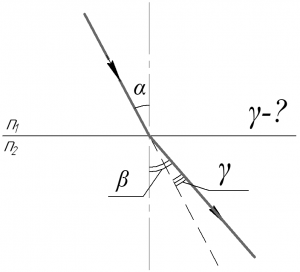Из рисунка к задаче прекрасно видно, что искомый угол \(\gamma\) следует искать по формуле:

\[\gamma = \beta — \alpha \;\;\;\;(1)\]

Запишем закон преломления света (также известен как закон преломления Снеллиуса):

\[{n_1}\sin \alpha = {n_2}\sin \beta \]

Здесь \(\alpha\) и \(\beta\) — угол падения и угол преломления соответственно, \(n_1\) и \(n_2\) — показатели преломления сред. Показатель преломления стекла \(n_1\) равен 1,5, показатель преломления воздуха \(n_2\) равен 1.

Тогда:

\[\sin \beta = \frac{{{n_1}\sin \alpha }}{{{n_2}}}\]

\[\beta = \arcsin \left( {\frac{{{n_1}\sin \alpha }}{{{n_2}}}} \right)\]

Полученное выражение подставим в формулу (1), окончательно получим:

\[\gamma = \arcsin \left( {\frac{{{n_1}\sin \alpha }}{{{n_2}}}} \right) — \alpha \]

Численный ответ задачи равен:

\[\gamma = \arcsin \left( {\frac{{1,5 \cdot \sin 30^\circ }}{1}} \right) — 30^\circ = 18,6^\circ \]