Условие задачи:

Небольшой предмет расположен между двумя плоскими зеркалами, образующими угол 30°. Предмет находится на расстоянии 10 см от линии пересечения зеркал и на одинаковом расстоянии от обоих зеркал. Каково расстояние между мнимыми изображениями этого предмета в зеркале?

Задача №10.1.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=30^\circ\), \(r=10\) см, \(l-?\)

Решение задачи:

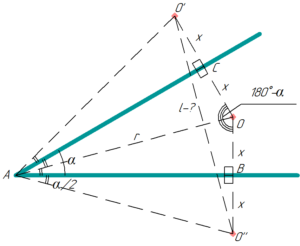Для решения задачи необходимо сделать рисунок. Важно понять, что предмет O расположен на биссектрисе AO угла BAC, образованного зеркалами, поскольку согласно условию он расположен на одинаковом расстоянии от обоих зеркал.

Далее необходимо построить изображения O’ и O» в обоих зеркалах, учитывая тот факт, что изображение предмета в плоском зеркале симметрично самому предмету относительно плоскости зеркала (поэтому OC=CO’=OB=BO»=x).

Из прямоугольного треугольника ACO найдем \(x\), учитывая, что угол CAO равен \(\frac{\alpha}{2}\), так как AO — биссектриса угла BAC:

\[x = r\sin \frac{\alpha }{2}\]

Теперь рассмотрим четырехугольник ABOС. Известно, что сумма углов выпуклого четырехугольника равна 360°. Так как углы ABO и ACO — прямые (т.е. равны 90°) и угол BAC равен \(\alpha\), то угол BOC равен \(\left( {180^\circ — \alpha } \right)\).

Отлично, осталось рассмотреть треугольник OO’O». Используя теорему косинусов, мы можем определить длину отрезка O’O», обозначенную у нас в решении как \(l\):

\[{l^2} = {\left( {2x} \right)^2} + {\left( {2x} \right)^2} — 2 \cdot 2x \cdot 2x \cdot \cos \left( {180^\circ — \alpha } \right)\]

\[{l^2} = 4{x^2} + 4{x^2} — 8{x^2} \cdot \cos \left( {180^\circ — \alpha } \right)\]

\[{l^2} = 8{x^2} — 8{x^2} \cdot \cos \left( {180^\circ — \alpha } \right)\]

Из тригонометрии известно, что \(\cos \left( {180^\circ — \alpha } \right) = — \cos \alpha\), поэтому:

\[{l^2} = 8{x^2} + 8{x^2} \cdot \cos \alpha \]

\[{l^2} = 8{x^2}\left( {1 + \cos \alpha } \right)\]

Также из тригонометрии известно, что \(\cos \alpha = 2{\cos^2}\frac{\alpha }{2} — 1\). Также учитывая ранее полученное выражение (1), имеем:

\[{l^2} = 8{r^2}{\sin ^2}\frac{\alpha }{2}\left( {1 + 2{\cos^2}\frac{\alpha }{2} — 1} \right)\]

\[{l^2} = 16{r^2}{\sin ^2}\frac{\alpha }{2}{\cos^2}\frac{\alpha }{2}\]

Так как \(\sin \alpha = 2\sin \frac{\alpha }{2}\cos \frac{\alpha }{2}\) (из той же тригонометрии, как Вы могли догадаться), то:

\[{l^2} = 4{r^2}{\sin ^2}\alpha \]

\[l = 2r\sin \alpha \]

Задача решена в общем виде, численный ответ задачи равен:

\[l = 2 \cdot 0,1 \cdot \sin 30^\circ = 0,1\;м\]

Ответ: 0,1 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

10.1.8 Солнечный луч, проходящий через отверстие в ставне, составляет с поверхностью стола
10.1.10 На какой высоте находится аэростат, если с башни высотой 20 м он виден под углом 45°
10.1.11 Какова должна быть минимальная высота вертикального зеркала, в котором человек