Решение: Небольшому шарику, который находится на поверхности горизонтально расположенной

Условие задачи:

Небольшому шарику, который находится на поверхности горизонтально расположенной собирающей линзы с оптической силой 0,5 дптр, сообщили вертикальную начальную скорость 10 м/с. Сколько времени будет существовать действительное изображение шарика в этой линзе?

Задача №10.5.71 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(D=0,5\) дптр, \(\upsilon_0=10\) м/с, \(\tau-?\)

Решение задачи:

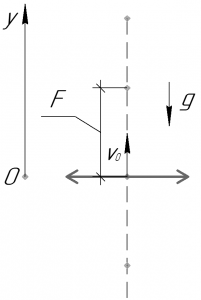Решающий эту задачу должен знать, что условие получения действительного изображения в собирающей линзе есть \({d} > {F}\), то есть предмет (в данном случае шарик) должен находиться от линзы на расстоянии больше фокусного. Получается, что нам нужно записать уравнение движения шарика, решив его, найти два времени, когда шарик будет на расстоянии \(F\), и далее из большего полученного времени вычесть меньшее, это и будет являться ответом этой задачи:

\[\tau = {t_2} — {t_1}\;\;\;\;(1)\]

Сразу определим фокусное расстояние собирающей силы \(F\) через её оптическую силу \(D\):

\[F = \frac{1}{D}\]

\[F = \frac{1}{{0,5}} = 2\;м\]

Запишем уравнение движения шарика по оси \(y\):

\[y = {\upsilon _0}t — \frac{{g{t^2}}}{2}\]

Решим это уравнение для случая \(y=F\):

\[F = {\upsilon _0}t — \frac{{g{t^2}}}{2}\]

Перенесем все члены в одну сторону:

\[\frac{{g{t^2}}}{2} — {\upsilon _0}t + F = 0\]

Посчитаем дискриминант:

\[{D_{диск}} = \upsilon _0^2 — 2gF\]

Посчитаем численное значение дискриминанта:

\[{D_{диск}} = {10^2} — 2 \cdot 10 \cdot 2 = 60 > 0\]

Получается, что квадратное уравнение имеет два корня, которые можно определить так:

\[t = \frac{{{\upsilon _0} \pm \sqrt {\upsilon _0^2 — 2gF} }}{g}\]

Таким образом, имеем:

\[{t_1} = \frac{{{\upsilon _0}}}{g} — \frac{{\sqrt {\upsilon _0^2 — 2gF} }}{g}\]

\[{t_2} = \frac{{{\upsilon _0}}}{g} + \frac{{\sqrt {\upsilon _0^2 — 2gF} }}{g}\]

Полученные выражения подставим в формулу (1):

\[\tau = \frac{{{\upsilon _0}}}{g} + \frac{{\sqrt {\upsilon _0^2 — 2gF} }}{g} — \frac{{{\upsilon _0}}}{g} + \frac{{\sqrt {\upsilon _0^2 — 2gF} }}{g}\]

\[\tau = \frac{{2\sqrt {\upsilon _0^2 — 2gF} }}{g}\]

Задача решена в общем виде, подставим численные данные задачи в полученную формулу и посчитаем численный ответ:

\[\tau = \frac{{2 \cdot \sqrt {{{10}^2} — 2 \cdot 10 \cdot 2} }}{{10}} = 1,55\;с\]