Решение: На расстоянии 60 см от собирающей линзы с фокусным расстоянием 50 см находится

Условие задачи:

На расстоянии 60 см от собирающей линзы с фокусным расстоянием 50 см находится точечный источник света. По другую сторону линзы расположено плоское зеркало, параллельное линзе. На каком расстоянии от линзы находится зеркало, если свет, отразившись от зеркала и пройдя через линзу, выходит параллельным пучком?

Задача №10.5.64 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(d=60\) см, \(F=50\) см, \(l-?\)

Решение задачи:

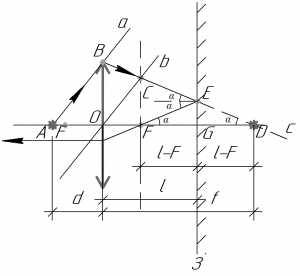Покажем общий принцип построения изображения точечного источника света в собирающей линзе. Чтобы построить изображение точечного источника света A в собирающей линзе, нужно провести через точку A произвольный луч a, этот луч в нашем случае пересечет линзу в точке B. Далее через главный оптический центр O проведем прямую b параллельную лучу a, которая пересечет заднюю фокальную плоскость в точке C. Далее необходимо провести через точки B и C прямую c, которая пересечет главную оптическую ось в точке D. Точка D и есть изображение точечного источника света A. Поскольку после линзы на пути луча встречается зеркало, то луч отразится от него в точке E. При этом отраженный луч должен пройти через задний фокус линзы, поскольку отраженный луч, пройдя через линзу, выходит параллельным пучком, как это сказано в условии задачи.

Понятно, что треугольники EFG и EGD равны по двум углам и стороне (EG), поэтому расстояние \(f\) можно записать как (смотрите рисунок):

\[f = F + \left( {l – F} \right) + \left( {l – F} \right)\]

\[f = 2l + F\]

\[l = \frac{F}{2} + \frac{f}{2}\;\;\;\;(1)\]

Запишем формулу тонкой линзы для того, чтобы определить неизвестное расстояние \(f\):

\[\frac{1}{F} = \frac{1}{d} + \frac{1}{f}\]

В этой формуле \(F\) – фокусное расстояние линзы, знак перед ним “+”, поскольку линза – собирающая, \(d\) – расстояние от линзы до предмета, знак перед ним “+”, поскольку предмет – действительный (в случае одиночной линзы предмет всегда действительный, оно бывает мнимым в случае системы линз), \(f\) – расстояние от линзы до изображения, знак перед ним “+”, поскольку изображение – действительное (то есть образуется на сходящемся пучке лучей – смотрите рисунок).

Выразим из формулы тонкой линзы расстояние \(f\):

\[\frac{1}{f} = \frac{1}{F} – \frac{1}{d}\]

\[\frac{1}{f} = \frac{{d – F}}{{dF}}\]

\[f = \frac{{dF}}{{d – F}}\;\;\;\;(2)\]

Подставим полученное выражение (2) в формулу (1):

\[l = \frac{F}{2} + \frac{{dF}}{{2\left( {d – F} \right)}}\]

Задача решена в общем, подставим в полученную формулу численные данные из условия задачи и посчитаем численный ответ:

\[l = \frac{{0,5}}{2} + \frac{{0,6 \cdot 0,5}}{{2\left( {0,6 – 0,5} \right)}} = 1,75\;м\]