Решение: На каком расстоянии от линзы с оптической силой 5 дптр необходимо поставить предмет

Условие задачи:

На каком расстоянии от линзы с оптической силой 5 дптр необходимо поставить предмет, чтобы его изображение было вдвое больше самого предмета?

Задача №10.5.15 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(D=5\) дптр, \(\Gamma = 2\), \(d-?\)

Решение задачи:

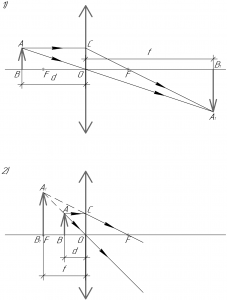Определенно ясно, что мы имеем дело с собирающей линзой, поскольку линза с положительной оптической силой является собирающей линзой. Но совершенно непонятно где находится предмет (и какого рода мы получаем изображение — действительное или мнимое), поэтому рассмотрим два случая (см. рисунок).

Случай первый — \({d} > {F}\) (но при этом \({d} < {2F}\), так как в противном случае мы не получим увеличенного изображения). Чтобы построить изображение точки A в собирающей линзе в данном случае, нужно провести через точку A два луча: один параллельно главной оптической оси, а второй через главный оптический центр O. Первый луч, преломившись в линзе, пройдет через задний фокус линзы. Второй луч проходит через линзу, не преломляясь. На пересечении этих лучей и будет находиться точка A₁. Проекция этой точки на главную оптическую ось есть точка B₁. Вот и все, изображение построено. Как мы видим, оно получилось действительным (поскольку получается на сходящемся пучке лучей), перевернутым и увеличенным (\(\Gamma > 1\)).

Запишем формулу тонкой линзы для этого случая:

\[D = \frac{1}{d} + \frac{1}{f}\;\;\;\;(1)\]

В этой формуле \(D\) — оптическая сила линзы, это положительная величина, поскольку линза — собирающая, \(d\) — расстояние от линзы до предмета, знак перед ним «+», поскольку предмет — действительный (в случае одиночной линзы предмет всегда действительный, оно бывает мнимым в случае системы линз), \(f\) — расстояние от линзы до изображения, знак перед ним «+», поскольку изображение — действительное (то есть образуется на сходящемся пучке лучей — смотрите рисунок).

Поперечное увеличение предмета в линзе \(\Gamma\) определяют по формуле (это можно вывести из подобия треугольников AOB и A₁OB₁):

\[\Gamma = \frac{f}{d}\]

Тогда:

\[f = \Gamma d\;\;\;\;(2)\]

Подставим выражение (2) в формулу (1):

\[D = \frac{1}{d} + \frac{1}{{\Gamma d}}\]

\[D = \frac{{\Gamma + 1}}{{\Gamma d}}\]

Откуда получим такую окончательную формулу:

\[d = \frac{{\Gamma + 1}}{{D\Gamma }}\]

Если подставить в эту формулу значения величин из условия задачи, то мы получим ответ (не забываем переводить эти значения в систему СИ):

\[d = \frac{{2 + 1}}{{5 \cdot 2}} = 0,3\;м\]

Случай второй — \({d} < {F}\). Чтобы построить изображение точки A в собирающей линзе в этом случае, нужно провести через точку A два луча: один параллельно главной оптической оси, а второй через главный оптический центр O. Первый луч, преломившись в линзе, пройдет через задний фокус линзы. Второй луч проходит через линзу, не преломляясь. Так как лучи не пересекаются, то их нужно продлить влево. На пересечении продолжений этих лучей и будет находиться точка A₁. Проекция этой точки на главную оптическую ось есть точка B₁. Вот и все, изображение построено. Как мы видим, оно получилось мнимым (поскольку получается на расходящемся пучке лучей), прямым и увеличенным (\(\Gamma > 1\)).

Запишем формулу тонкой линзы для данного случая:

\[D = \frac{1}{d} — \frac{1}{f}\;\;\;\;(3)\]

В этой формуле \(D\) — оптическая сила линзы, знак перед ней «+», поскольку линза — собирающая, \(d\) — расстояние от линзы до предмета, знак перед ним «+», поскольку предмет — действительный (в случае одиночной линзы предмет всегда действительный, оно бывает мнимым в случае системы линз), \(f\) — расстояние от линзы до изображения, знак перед ним «-«, поскольку изображение — мнимое (то есть образуется на расходящемся пучке лучей — смотрите рисунок).

Аналогично, поперечное увеличение предмета в линзе \(\Gamma\) определяют по формуле (это можно вывести из подобия треугольников AOB и A₁OB₁):

\[\Gamma = \frac{f}{d}\]

Тогда:

\[f = \Gamma d\;\;\;\;(4)\]

Подставим выражение (4) в формулу (3):

\[D = \frac{1}{d} — \frac{1}{{\Gamma d}}\]

Приведем под общий знаменатель в правой части полученного уравнения:

\[D = \frac{{\Gamma — 1}}{{\Gamma d}}\]

Тогда:

\[d = \frac{{\Gamma — 1}}{{D\Gamma }}\]

Численный ответ в этом случае равен:

\[d = \frac{{2 — 1}}{{5 \cdot 2}} = 0,1\;м\]