Решение: На дифракционную решетку с периодом 6 мкм падает монохроматическая волна

Условие задачи:

На дифракционную решетку с периодом 6 мкм падает монохроматическая волна. Определить длину волны, если угол между дифракционными максимумами второго и третьего порядка равен 3°. Углы дифракции считать малыми.

Задача №10.7.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(d=6\) мкм, \(k_1=2\), \(k_2=3\), \(\Delta \varphi = 3^\circ\), \(\lambda-?\)

Решение задачи:

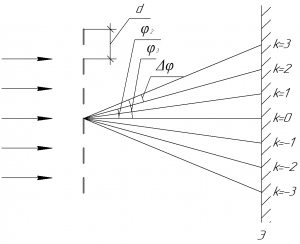Вспомним формулу дифракционной решетки:

\[d\sin \varphi = k\lambda\;\;\;\;(1)\]

В этой формуле \(d\) — период решетки (также называют постоянной решетки), \(\varphi\) — угол дифракции, \(k\) — порядок максимума, \(\lambda\) — длина волны, падающей нормально на решетку.

Запишем формулу (1) для второго и третьего максимумов (\(k_1=2\) и \(k_2=2\)):

\[\left\{ \begin{gathered}
d\sin {\varphi _1} = {k_1}\lambda \hfill \\
d\sin {\varphi _2} = {k_2}\lambda \hfill \\
\end{gathered} \right.\]

В условии говорится, что углы дифракции можно считать малыми, поэтому справедлив переход от синусов углов к самим углам, то есть:

\[\sin \varphi \approx \varphi \]

Тогда:

\[\left\{ \begin{gathered}
d{\varphi _1} = {k_1}\lambda \hfill \\
d{\varphi _2} = {k_2}\lambda \hfill \\
\end{gathered} \right.\]

Вычтем из нижнего уравнения верхнее:

\[d\left( {{\varphi _2} — {\varphi _1}} \right) = \left( {{k_2} — {k_1}} \right)\lambda \]

Разность углов дифракции для третьего и второго порядков есть угол между максимумами третьего и второго порядка \(\Delta \varphi\), который дан в условии, поэтому:

\[d\Delta \varphi = \left( {{k_2} — {k_1}} \right)\lambda \]

Откуда искомая длина волны падающего света \(\lambda\) равна:

\[\lambda = \frac{{d\Delta \varphi }}{{{k_2} — {k_1}}}\]

Задача решена в общем виде, подставим данные из условия в полученную формулу и посчитаем численный ответ (угол \(\Delta \varphi\) обязательно должен быть переведен в радианы, для чего его нужно умножить на \(\pi\) и разделить на 180°):

\[\lambda = \frac{{6 \cdot {{10}^{ — 6}} \cdot 3^\circ \cdot 3,14}}{{\left( {3 — 2} \right) \cdot 180^\circ }} = 314 \cdot {10^{ — 9}}\;м = 314\;нм\]