Условие задачи:

Луч света падает под углом 30° на плоскопараллельную стеклянную пластинку и выходит из нее параллельно первоначальному лучу. Показатель преломления стекла равен 1,5. Какова толщина пластинки, если расстояние между лучами 1,94 см?

Задача №10.3.34 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=30^\circ\), \(n_2=1,5\), \(l=1,94\) см, \(d-?\)

Решение задачи:

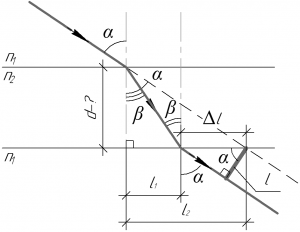Разумеется к такой задаче необходимо сделать хороший рисунок, без него решить задачу невозможно. Первое, что можно увидеть на рисунке, так это то, что смещение \(l\) можно найти из прямоугольного треугольника по формуле:

\[l = \Delta l\cos \alpha\;\;\;\;(1)\]

Расстояние \(\Delta l\) можно определить следующим образом:

\[\Delta l = {l_2} — {l_1}\]

Расстояния \(l_1\) и \(l_2\) можно найти из соответствующих прямоугольных треугольников (да, опять) по следующим формулам:

\[\left\{ \begin{gathered}
{l_1} = d \cdot tg\beta \hfill \\
{l_2} = d \cdot tg\alpha \hfill \\
\end{gathered} \right.\]

Учитывая все вышесказанное, формула (1) примет вид:

\[l = d\cos \alpha \left( {tg\alpha — tg\beta } \right)\;\;\;\;(2)\]

Чтобы найти угол преломления \(\beta\), запишем закон преломления света (также известен как закон преломления Снеллиуса):

\[{n_1}\sin \alpha = {n_2}\sin \beta\]

Здесь \(\alpha\) и \(\beta\) — угол падения и угол преломления соответственно, \(n_1\) и \(n_2\) — показатели преломления сред. Показатель преломления воздуха \(n_1\) равен 1, показатель преломления стекла \(n_2\) равен 1,5.

Тогда:

\[\sin \beta = \frac{{{n_1}\sin \alpha }}{{{n_2}}}\]

\[\beta = \arcsin \left( {\frac{{{n_1}\sin \alpha }}{{{n_2}}}} \right)\;\;\;\;(3)\]

Подставим выражение (3) в формулу (2):

\[l = d\cos \alpha \left( {tg\alpha — tg\left( {\arcsin \left( {\frac{{{n_1}\sin \alpha }}{{{n_2}}}} \right)} \right)} \right)\]

Откуда искомая толщина пластинки \(d\) равна:

\[d = \frac{l}{{\cos \alpha \left( {tg\alpha — tg\left( {\arcsin \left( {\frac{{{n_1}\sin \alpha }}{{{n_2}}}} \right)} \right)} \right)}}\]

Задача решена в общем виде, подставим данные задачи в полученную формулу и посчитаем численный ответ:

\[d = \frac{{0,0194}}{{\cos 30^\circ \cdot \left( {tg30^\circ — tg\left( {\arcsin \left( {\frac{{1 \cdot \sin 30^\circ }}{{1,5}}} \right)} \right)} \right)}} = 0,1\;м = 10\;см\]

Ответ: 10 см.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

10.3.33 Определить смещение светового луча при прохождении его через стеклянную пластинку
10.3.35 Луч света падает перпендикулярно на вертикальную грань прозрачной призмы
10.3.36 Показатель преломления стекла призмы для красных лучей равен 1,483. Преломляющий