Условие задачи:

Линзой пользуются как лупой. Первоначально изображение было в 4 раза больше предмета. Затем лупу отодвинули от предмета на 0,4 см, после чего изображение стало в 5 раз больше предмета. Определить оптическую силу линзы.

Задача №10.5.67 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\Gamma_1=4\), \(\Delta d=0,4\) см, \(\Gamma_2=5\), \(D-?\)

Решение задачи:

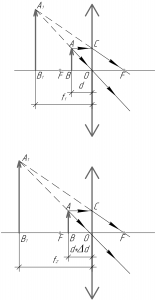Мы имеем дело с собирающей линзой, поскольку рассеивающая линза не может давать увеличенного изображения. При этом расстояние от предмета до линзы в обоих случаях должно быть меньше фокусного расстояния (так как линзой пользуются как лупой), т.е. предмет находится правее переднего фокуса линзы. В случае \({d} < {F}\) при увеличении расстояния от линзы до предмета поперечное увеличение линзы, даваемое линзой, будет увеличиваться, как и говорится в условии задачи.

Покажем общий принцип построения изображения в собирающей линзе. Чтобы построить изображение точки A в собирающей линзе в данном случае, нужно провести через точку A два луча: один параллельно главной оптической оси, а второй через главный оптический центр O. Первый луч, преломившись в линзе, пройдет через задний фокус линзы. Второй луч проходит через линзу, не преломляясь. На пересечении продолжений этих лучей и будет находиться точка A₁. Проекция этой точки на главную оптическую ось есть точка B₁. Вот и все, изображение построено. Как мы видим, оно получилось мнимым (поскольку получается на расходящемся пучке лучей) и прямым.

Запишем формулу тонкой линзы для собирающей линзы для случая, когда линза дает мнимое изображение:

\[D = \frac{1}{d} — \frac{1}{f}\;\;\;\;(1)\]

В этой формуле \(D\) — оптическая сила линзы, это положительная величина, поскольку линза — собирающая, \(d\) — расстояние от линзы до предмета, знак перед ним «+», поскольку предмет — действительный (в случае одиночной линзы предмет всегда действительный, оно бывает мнимым в случае системы линз), \(f\) — расстояние от линзы до изображения, знак перед ним «-«, поскольку изображение — мнимое (то есть образуется на расходящемся пучке лучей — смотрите рисунок).

Запишем формулу (1) для двух случаев, описанных в условии задачи:

\[\left\{ \begin{gathered}
D = \frac{1}{d} — \frac{1}{{{f_1}}} \hfill \\
D = \frac{1}{{d + \Delta d}} — \frac{1}{{{f_2}}} \hfill \\
\end{gathered} \right.\]

Известно, что поперечное увеличение линзы можно найти \(\Gamma\) можно выразить как отношение расстояния от линзы до экрана \(f\) к расстоянию от предмета до линзы \(d\), то есть:

\[\Gamma = \frac{f}{d} \Rightarrow f = \Gamma d\;\;\;\;(2)\]

Учитывая (2), система примет вид:

\[\left\{ \begin{gathered}
D = \frac{1}{d} — \frac{1}{{{\Gamma _1}d}} \hfill \\
D = \frac{1}{{d + \Delta d}} — \frac{1}{{{\Gamma _2}\left( {d + \Delta d} \right)}} \hfill \\
\end{gathered} \right.\]

\[\left\{ \begin{gathered}
D = \frac{{{\Gamma _1} — 1}}{{{\Gamma _1}d}} \;\;\;\;(3)\hfill \\
D = \frac{{{\Gamma _2} — 1}}{{{\Gamma _2}\left( {d + \Delta d} \right)}} \hfill \\
\end{gathered} \right.\]

Имеем следующее уравнение:

\[\frac{{{\Gamma _1} — 1}}{{{\Gamma _1}d}} = \frac{{{\Gamma _2} — 1}}{{{\Gamma _2}\left( {d + \Delta d} \right)}}\]

Перемножим «крест-накрест»:

\[{\Gamma _1}d\left( {{\Gamma _2} — 1} \right) = {\Gamma _2}\left( {{\Gamma _1} — 1} \right)\left( {d + \Delta d} \right)\]

\[{\Gamma _1}d\left( {{\Gamma _2} — 1} \right) = {\Gamma _2}\left( {{\Gamma _1}d + {\Gamma _1}\Delta d — d — \Delta d} \right)\]

Раскроем все скобки в обеих частях уравнения:

\[{\Gamma _1}{\Gamma _2}d — {\Gamma _1}d = {\Gamma _1}{\Gamma _2}d + {\Gamma _1}{\Gamma _2}\Delta d — {\Gamma _2}d — {\Gamma _2}\Delta d\]

\[{\Gamma _1}{\Gamma _2}\Delta d — {\Gamma _2}\Delta d = {\Gamma _2}d — {\Gamma _1}d\]

\[{\Gamma _2}\Delta d\left( {{\Gamma _1} — 1} \right) = d\left( {{\Gamma _2} — {\Gamma _1}} \right)\]

\[d = \frac{{{\Gamma _2}\Delta d\left( {{\Gamma _1} — 1} \right)}}{{{\Gamma _2} — {\Gamma _1}}}\]

Осталось только полученное выражение подставить в уравнение (3):

\[D = \frac{{{\Gamma _1} — 1}}{{{\Gamma _1}}} \cdot \frac{{{\Gamma _2} — {\Gamma _1}}}{{{\Gamma _2}\Delta d\left( {{\Gamma _1} — 1} \right)}}\]

\[D = \frac{{{\Gamma _2} — {\Gamma _1}}}{{{\Gamma _1}{\Gamma _2}\Delta d}}\]

Посчитаем численный ответ данной задачи:

\[D = \frac{{5 — 4}}{{4 \cdot 5 \cdot 0,004}} = 12,5\;дптр\]

Ответ: 12,5 дптр.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

10.5.66 Фотоаппаратом с расстояния 500 м сделан снимок телебашни. Фокусное расстояние
10.5.68 С самолета, летящего на высоте 12 км, сфотографирована местность в масштабе 1:16000
10.5.69 При фотографировании предмета с расстояния 1 м высота изображения равна 6 см