Условие задачи:
Линза дает действительное изображение предмета с увеличением 3. Какое увеличение даст линза с оптической силой в 2 раза меньше, если расстояние между линзой и предметом будет то же самое?
Задача №10.5.22 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\Gamma_1 = 3\), \(D_2 = \frac{D_1}{2}\), \(d_1=d_2\), \(\Gamma_2-?\)
Решение задачи:
Оптическая сила \(D\) связана с фокусным расстоянием \(F\) обратной зависимостью, то есть:
\[D = \frac{1}{F}\]
Так как по условию задачи \(D_2 = \frac{D_1}{2}\), то:
\[\frac{1}{{{F_2}}} = \frac{1}{{2{F_1}}}\]
\[{F_2} = 2{F_1}\]
 Получается, что у второй линзы фокусное расстояние \(F_2\) в два раза больше, чем у первой линзы.
Получается, что у второй линзы фокусное расстояние \(F_2\) в два раза больше, чем у первой линзы.
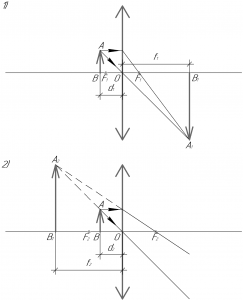
Собирающая линза дает действительное изображение с увеличением, если предмет находится между фокусом и двойным фокусом, то есть для первой линзы выполняется условие \({F_1} < {d_1} < {2F_1}\). Учитывая, что \({F_2} = 2{F_1}\) и \(d_1=d_2\), для второй линзы будет выполняться следующее условие — \(\frac{F_2}{2} < {d_2} < {F_2}\). Получается, что вторая линза будет уже давать мнимое прямое изображение.
Вопрос построения изображений предмета в собирающих линзах опустим (смотрите другие задачи), а сразу запишем формулу тонкой линзы применительно для этих двух случаев:
\[\left\{ \begin{gathered}
\frac{1}{{{F_1}}} = \frac{1}{{{d_1}}} + \frac{1}{{{f_1}}} \hfill \\
\frac{1}{{{F_2}}} = \frac{1}{{{d_2}}} — \frac{1}{{{f_2}}} \hfill \\
\end{gathered} \right.\]
В этих формулах:
- \(F_1\) и \(F_2\) — фокусные расстояния линз, знак перед ними «+», поскольку линзы — собирающие;
- \(d_1\) и \(d_2\) — расстояния от линз до предмета, знак перед ними «+», поскольку предмет — действительный (в случае одиночных линз предмет всегда действительный, оно бывает мнимым в случае системы линз);
- \(f_1\) и \(f_2\) — расстояния от линз до изображений, знак перед ними «+», если изображение — действительное (то есть образуется на сходящемся пучке лучей), иначе — «-«, то есть изображение — мнимое (то есть образуется на расходящемся пучке лучей).
В общем случае поперечное увеличение предмета в линзе \(\Gamma\) определяют по формуле (это можно вывести из подобия треугольников AOB и A1OB1):
\[\Gamma = \frac{f}{d}\]
Поэтому:
\[\left\{ \begin{gathered}
{f_1} = {\Gamma _1}{d_1} \hfill \\
{f_2} = {\Gamma _2}{d_2} \hfill \\
\end{gathered} \right.\]
Тогда:
\[\left\{ \begin{gathered}
\frac{1}{{{F_1}}} = \frac{1}{{{d_1}}} + \frac{1}{{{\Gamma _1}{d_1}}} \hfill \\
\frac{1}{{{F_2}}} = \frac{1}{{{d_2}}} — \frac{1}{{{\Gamma _2}{d_2}}} \hfill \\
\end{gathered} \right.\]
Так как \({F_2} = 2{F_1}\) и \(d_1=d_2\), имеем:
\[\left\{ \begin{gathered}
\frac{1}{{{F_1}}} = \frac{1}{{{d_1}}} + \frac{1}{{{\Gamma _1}{d_1}}} \hfill \\
\frac{1}{{2{F_1}}} = \frac{1}{{{d_1}}} — \frac{1}{{{\Gamma _2}{d_1}}} \hfill \\
\end{gathered} \right.\]
Обе части нижнего уравнения умножим на 2:
\[\left\{ \begin{gathered}
\frac{1}{{{F_1}}} = \frac{1}{{{d_1}}} + \frac{1}{{{\Gamma _1}{d_1}}} \hfill \\
\frac{1}{{{F_1}}} = \frac{2}{{{d_1}}} — \frac{2}{{{\Gamma _2}{d_1}}} \hfill \\
\end{gathered} \right.\]
В таком случае:
\[\frac{1}{{{d_1}}} + \frac{1}{{{\Gamma _1}{d_1}}} = \frac{2}{{{d_1}}} — \frac{2}{{{\Gamma _2}{d_1}}}\]
Видно, что можно сократить на \(d_1\) обе части уравнения:
\[1 + \frac{1}{{{\Gamma _1}}} = 2 — \frac{2}{{{\Gamma _2}}}\]
\[\frac{1}{{{\Gamma _1}}} + \frac{2}{{{\Gamma _2}}} = 1\]
\[\frac{2}{{{\Gamma _2}}} = 1 — \frac{1}{{{\Gamma _1}}}\]
\[\frac{2}{{{\Gamma _2}}} = \frac{{{\Gamma _1} — 1}}{{{\Gamma _1}}}\]
Окончательно получим следующее решение задачи в общем виде:
\[{\Gamma _2} = \frac{{2{\Gamma _1}}}{{{\Gamma _1} — 1}}\]
Численный ответ задачи равен:
\[{\Gamma _2} = \frac{{2 \cdot 3}}{{3 — 1}} = 3\]
Ответ: 3.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.5.21 Расстояние от предмета до экрана 5 м. Какой оптической силы надо взять линзу
10.5.23 Предмет находится на расстоянии 0,1 м от переднего фокуса собирающей линзы
10.5.24 Точечный источник света находится на расстоянии 50 см от собирающей линзы