Решение: Кубический сосуд с непрозрачными стенками расположен так, что глаз наблюдателя

Условие задачи:

Кубический сосуд с непрозрачными стенками расположен так, что глаз наблюдателя не видит его дна, но полностью видит заднюю вертикальную стенку. Сколько воды нужно налить в сосуд, чтобы наблюдатель смог увидеть предмет, находящийся на расстоянии 10 см от задней стенки сосуда на его дне? Ребро сосуда 40 см.

Задача №10.3.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(l=10\) см, \(a=40\) см, \(V-?\)

Решение задачи:

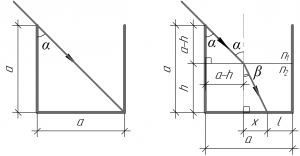Разумеется, сначала нужно сделать рисунки к задаче. Рассмотрим рисунок слева, он поможет нам найти угол падения луча \(\alpha\). Так как сосуд имеет форму куба, то синус угла \(\alpha\) можно найти следующим образом:

\[\sin \alpha = \frac{a}{{\sqrt {{a^2} + {a^2}} }}\]

\[\sin \alpha = \frac{{\sqrt 2 }}{2}\;\;\;\;(1)\]

Теперь займемся правым рисунком. Из равенства (1) следует, что угол \(\alpha\) равен 45°, и это очень важный вывод. Значит в прямоугольном треугольнике, образованном лучом, стенкой сосуда и поверхностью воды, оба катета равны \(\left( {a — h} \right)\) (смотрите рисунок справа).

Для ситуации на рисунке справа запишем закон преломления света (также известен как закон преломления Снеллиуса):

\[{n_1}\sin \alpha = {n_2}\sin \beta\;\;\;\;(2)\]

Здесь \(\alpha\) и \(\beta\) — угол падения и угол преломления соответственно, \(n_1\) и \(n_2\) — показатели преломления сред. Показатель преломления воздуха \(n_1\) равен 1, показатель преломления воды \(n_2\) равен 1,33.

Попытаемся найти синус угла \(\beta\), для чего найдем противолежащий катет \(x\) в соответствующем прямоугольном треугольнике.

\[x = a — l — \left( {a — h} \right)\]

\[x = h — l\]

Сделаем важную оговорку: так как \(x\) не может быть меньше нуля, то \({h} > {l}\), это пригодится нам в дальнейшем решении.

Тогда синус угла \(\beta\) найдем по формуле (гипотенузу в том же прямоугольном треугольнике найдем по теореме Пифагора):

\[\sin \beta = \frac{{h — l}}{{\sqrt {{{\left( {h — l} \right)}^2} + {h^2}} }}\;\;\;\;(3)\]

Подставим в уравнение (2) выражения (1) и (3):

\[\frac{{\sqrt 2 {n_1}}}{2} = \frac{{{n_2}\left( {h — l} \right)}}{{\sqrt {{{\left( {h — l} \right)}^2} + {h^2}} }}\]

Как Вы должны понимать, физика в этой задаче закончилась, осталась только математика — нужно решить данное уравнение. Перепишем его в следующем виде:

\[\frac{{\sqrt 2 {n_1}}}{{2{n_2}}} = \frac{{h — l}}{{\sqrt {{{\left( {h — l} \right)}^2} + {h^2}} }}\]

Возведем в квадрат обе части этого уравнения:

\[\frac{{n_1^2}}{{2n_2^2}} = \frac{{{{\left( {h — l} \right)}^2}}}{{{{\left( {h — l} \right)}^2} + {h^2}}}\]

Перемножим «крест-накрест»:

\[n_1^2{\left( {h — l} \right)^2} + n_1^2{h^2} = 2n_2^2{\left( {h — l} \right)^2}\]

Раскроем скобки в обеих частях уравнения:

\[n_1^2{h^2} — 2n_1^2hl + n_1^2{l^2} + n_1^2{h^2} = 2n_2^2{h^2} — 4n_2^2hl + 2n_2^2{l^2}\]

Перенесем все в правую часть и сгруппируем:

\[\left( {2n_2^2 — 2n_1^2} \right){h^2} — \left( {4n_2^2 — 2n_1^2} \right)hl + \left( {2n_2^2 — n_1^2} \right){l^2} = 0\]

Поделим все на \(l^2\):

\[\left( {2n_2^2 — 2n_1^2} \right){\left( {\frac{h}{l}} \right)^2} — \left( {4n_2^2 — 2n_1^2} \right)\left( {\frac{h}{l}} \right) + \left( {2n_2^2 — n_1^2} \right) = 0\]

Решим данное квадратное уравнение относительно \(\frac{h}{l}\), для чего перейдем к нахождению дискриминанта:

\[D = {\left( {4n_2^2 — 2n_1^2} \right)^2} — 4\left( {2n_2^2 — 2n_1^2} \right)\left( {2n_2^2 — n_1^2} \right)\]

Раскрываем скобки:

\[D = 16n_2^4 — 16n_1^2n_2^2 + 4n_1^4 — 16n_2^4 + 8n_1^2n_2^2 + 16n_1^2n_2^2 — 8n_1^4\]

\[D = 8n_1^2n_2^2 — 4n_1^4\]

\[D = 4n_1^2\left( {2n_2^2 — n_1^2} \right)\]

Учитывая численные значения показателей преломления, нетрудно сделать вывод, что дискриминант — положительный. Тогда корни уравнения следующие:

\[\frac{h}{l} = \frac{{4n_2^2 — 2n_1^2 \pm \sqrt {4n_1^2\left( {2n_2^2 — n_1^2} \right)} }}{{2\left( {2n_2^2 — 2n_1^2} \right)}}\]

\[\frac{h}{l} = \frac{{4n_2^2 — 2n_1^2 \pm 2{n_1}\sqrt {2n_2^2 — n_1^2} }}{{2\left( {2n_2^2 — 2n_1^2} \right)}}\]

Посчитаем численное значение корней:

\[\left[ \begin{gathered}
\frac{h}{l} = \frac{{4 \cdot {{1,33}^2} — 2 \cdot {1^2} + 2 \cdot 1 \cdot \sqrt {2 \cdot {{1,33}^2} — {1^2}} }}{{2\left( {2 \cdot {{1,33}^2} — 2 \cdot {1^2}} \right)}} = 2,686 \hfill \\
\frac{h}{l} = \frac{{4 \cdot {{1,33}^2} — 2 \cdot {1^2} — 2 \cdot 1 \cdot \sqrt {2 \cdot {{1,33}^2} — {1^2}} }}{{2\left( {2 \cdot {{1,33}^2} — 2 \cdot {1^2}} \right)}} = 0,614 \hfill \\
\end{gathered} \right.\]

Как Вы видите, второй корень не удовлетворяют условию \({h} > {l}\). Значит уровень воды \(h\) равен:

\[h = \left( {\frac{{4n_2^2 — 2n_1^2 + 2{n_1}\sqrt {2n_2^2 — n_1^2} }}{{2\left( {2n_2^2 — 2n_1^2} \right)}}} \right)l\]

Искомый объем воды легко найти по формуле:

\[V = {a^2}h\]

Окончательно получим:

\[V = \left( {\frac{{4n_2^2 — 2n_1^2 + 2{n_1}\sqrt {2n_2^2 — n_1^2} }}{{2\left( {2n_2^2 — 2n_1^2} \right)}}} \right){a^2}l\]

\[V = \left( {\frac{{4 \cdot {{1,33}^2} — 2 \cdot {1^2} + 2 \cdot 1 \cdot \sqrt {2 \cdot {{1,33}^2} — {1^2}} }}{{2\left( {2 \cdot {{1,33}^2} — 2 \cdot {1^2}} \right)}}} \right) \cdot {0,4^2} \cdot 0,1 = 0,043\;м^3 = 43\;л\]