Решение: Какова истинная глубина водоема, если камень, лежащий на дне его, при рассматривании

Условие задачи:

Какова истинная глубина водоема, если камень, лежащий на дне его, при рассматривании по вертикали, кажется находящимся на расстоянии 1,5 м?

Задача №10.3.41 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(h=1,5\) м, \(H-?\)

Решение задачи:

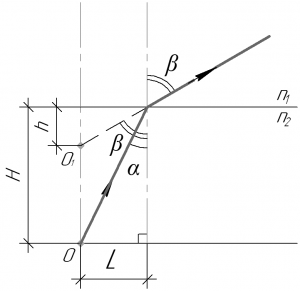Для решения задачи сделаем рисунок. При этом для решения этой задачи нам нужно рассмотреть ход параксиального луча, то есть луча, который распространяется под малым углом к оси OO₁. На рисунке углы \(\alpha\) и \(\beta\) не являются малыми, это сделано исключительно для наглядности рисунка.

Запишем закон преломления света (также известен как закон преломления Снеллиуса):

\[{n_2}\sin \alpha = {n_1}\sin \beta\]

Здесь \(\alpha\) и \(\beta\) — угол падения и угол преломления соответственно, \(n_1\) и \(n_2\) — показатели преломления сред. Показатель преломления воздуха \(n_1\) равен 1, показатель преломления воды \(n_2\) равен 1,33.

Так как углы \(\alpha\) и \(\beta\) являются малыми, тогда можно воспользоваться тем, что в таком случае \(\sin \alpha \approx \alpha\) и \(\sin \beta \approx \beta\) (здесь углы, разумеется, выражены в радианах). Тогда:

\[{n_2}\alpha = {n_1}\beta \]

\[\beta = \frac{{{n_2}}}{{{n_1}}}\alpha \;\;\;\;(1)\]

Также из прямоугольных треугольников можно получить следующее:

\[\left\{ \begin{gathered}
tg\alpha = \frac{L}{H} \hfill \\
tg\beta = \frac{L}{h} \hfill \\
\end{gathered} \right.\]

Имеем:

\[\left\{ \begin{gathered}
L = H \cdot tg\alpha \hfill \\
L = h \cdot tg\beta \hfill \\
\end{gathered} \right.\]

\[H \cdot tg\alpha = h \cdot tg\beta \]

Опять же, если углы \(\alpha\) и \(\beta\) являются малыми, тогда можно воспользоваться тем, что в таком случае \(tg \alpha \approx \alpha\) и \(tg \beta \approx \beta\) (здесь углы, разумеется, выражены в радианах).

\[H \cdot \alpha = h \cdot \beta \]

В полученное уравнение подставим выражение (1):

\[H \cdot \alpha = h \cdot \frac{{{n_2}}}{{{n_1}}}\alpha \]

\[H = \frac{{{n_2}}}{{{n_1}}}h\]

Задача решена в общем, подставим данные задачи в полученную формулу и посчитаем численный ответ:

\[H = \frac{{1,33}}{1} \cdot 1,5 = 2\;м\]