Решение: Какова глубина бассейна, если человек, глядя под углом 30° к поверхности воды

Условие задачи:

Какова глубина бассейна, если человек, глядя под углом 30° к поверхности воды, видит монету, лежащую на дне на расстоянии 0,50 м дальше, чем на самом деле?

Задача №10.3.40 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\gamma=30^\circ\), \(L=0,5\) м, \(H-?\)

Решение задачи:

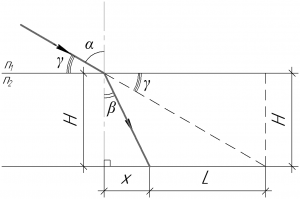Для решения задачи нужно обязательно сделать рисунок.

Запишем закон преломления света (также известен как закон преломления Снеллиуса):

\[{n_1}\sin \alpha = {n_2}\sin \beta\]

Здесь \(\alpha\) и \(\beta\) – угол падения и угол преломления соответственно, \(n_1\) и \(n_2\) – показатели преломления сред. Показатель преломления воздуха \(n_1\) равен 1, показатель преломления воды \(n_2\) равен 1,33.

Так как \(\alpha = 90^\circ – \gamma\) и \(\sin \left( {90^\circ – \gamma } \right) = \cos \gamma\), то имеем:

\[{n_1}\sin \left( {90^\circ – \gamma } \right) = {n_2}\sin \beta \]

\[{n_1}\cos \gamma = {n_2}\sin \beta\;\;\;\;(1)\]

Из рисунка видно, что синус угла \(\beta\) равен:

\[\sin \beta = \frac{x}{{\sqrt {{x^2} + {H^2}} }}\]

В таком случае формула (1) примет вид:

\[{n_1}\cos \gamma = \frac{{{n_2}x}}{{\sqrt {{x^2} + {H^2}} }}\]

Возведем в квадрат обе части этого уравнения:

\[n_1^2{\cos ^2}\gamma = \frac{{n_2^2{x^2}}}{{{x^2} + {H^2}}}\]

Тогда:

\[n_1^2{\cos ^2}\gamma \left( {{x^2} + {H^2}} \right) = n_2^2{x^2}\]

Раскроем скобки:

\[n_1^2{x^2}{\cos ^2}\gamma + n_1^2{H^2}{\cos ^2}\gamma = n_2^2{x^2}\]

Часть слагаемых перенесем в правую часть уравнения:

\[n_1^2{H^2}{\cos ^2}\gamma = n_2^2{x^2} – n_1^2{x^2}{\cos ^2}\gamma \]

Вынесем за скобки \(x^2\):

\[n_1^2{H^2}{\cos ^2}\gamma = {x^2}\left( {n_2^2 – n_1^2{{\cos }^2}\gamma } \right)\]

Выразим \(x^2\):

\[{x^2} = \frac{{n_1^2{H^2}{{\cos }^2}\gamma }}{{n_2^2 – n_1^2{{\cos }^2}\gamma }}\]

Извлечем квадратный корень из обеих частей уравнения:

\[x = \frac{{{n_1}H\cos \gamma }}{{\sqrt {n_2^2 – n_1^2{{\cos }^2}\gamma } }}\;\;\;\;(2)\]

Также из рисунка видно, что:

\[tg\gamma = \frac{H}{{x + L}}\]

Тогда имеем следующее:

\[\left( {x + L} \right)tg\gamma = H\]

\[xtg\gamma + Ltg\gamma = H\]

Учитывая (2), имеем:

\[\frac{{{n_1}H\cos \gamma }}{{\sqrt {n_2^2 – n_1^2{{\cos }^2}\gamma } }}tg\gamma + Ltg\gamma = H\]

Поскольку \(\sin \gamma = \cos \gamma \cdot tg\gamma\), то:

\[\frac{{{n_1}H\sin \gamma }}{{\sqrt {n_2^2 – n_1^2{{\cos }^2}\gamma } }} + Ltg\gamma = H\]

Все слагаемые с множителем \(H\) перенесем в одну сторону:

\[Ltg\gamma = H – \frac{{{n_1}H\sin \gamma }}{{\sqrt {n_2^2 – n_1^2{{\cos }^2}\gamma } }}\]

\[Ltg\gamma = H\left( {1 – \frac{{{n_1}\sin \gamma }}{{\sqrt {n_2^2 – n_1^2{{\cos }^2}\gamma } }}} \right)\]

Приведем под общий знаменатель в скобках:

\[Ltg\gamma = H\left( {\frac{{\sqrt {n_2^2 – n_1^2{{\cos }^2}\gamma } – {n_1}\sin \gamma }}{{\sqrt {n_2^2 – n_1^2{{\cos }^2}\gamma } }}} \right)\]

\[H = \frac{{Ltg\gamma \sqrt {n_2^2 – n_1^2{{\cos }^2}\gamma } }}{{\sqrt {n_2^2 – n_1^2{{\cos }^2}\gamma } – {n_1}\sin \gamma }}\]

Задача решена в общем, подставим данные задачи в полученную формулу и посчитаем численный ответ:

\[H = \frac{{0,5 \cdot tg30^\circ \cdot \sqrt {{{1,33}^2} – {1^2} \cdot {{\cos }^2}30^\circ } }}{{\sqrt {{{1,33}^2} – {1^2} \cdot {{\cos }^2}30^\circ } – 1 \cdot \sin 30^\circ }} = 0,572\;м\]