Условие задачи:
Изображение светящейся точки в рассеивающей линзе с оптической силой \(D=-5\) дптр находится в два раза ближе к линзе, чем сама точка, находящаяся на главной оптической оси. Найти расстояние светящейся точки от линзы.
Задача №10.5.60 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(D=-5\) дптр, \(f=\frac{d}{2}\), \(d-?\)
Решение задачи:
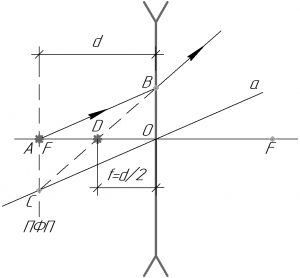Покажем общий принцип построения изображения точечного источника света в рассеивающей линзе. Чтобы построить изображение точечного источника света A в рассеивающей линзе, нужно провести из точки A произвольный луч, этот луч пересечет линзу в точке B, как видно на рисунке. Далее через главный оптический центр O проведем прямую a параллельную лучу AB, которая пересечет переднюю фокальную плоскость в точке C. Далее необходимо провести через точки B и C прямую, которая пересечет главную оптическую ось в точке D. Точка D и есть изображение точечного источника света A.
Запишем формулу тонкой линзы:
\[D = \frac{1}{d} – \frac{1}{f}\;\;\;\;(1)\]
В этой формуле \(D\) – оптическая силы линзы, это величина отрицательная, поскольку линза – рассеивающая, \(d\) – расстояние от линзы до предмета, знак перед ним “+”, поскольку предмет – действительный (в случае одиночной линзы предмет всегда действительный, оно бывает мнимым в случае системы линз), \(f\) – расстояние от линзы до изображения, знак перед ним “-“, поскольку изображение – мнимое (то есть образуется на расходящемся пучке лучей – смотрите рисунок).
Так как по условию \(f=\frac{d}{2}\), то формула (1) примет вид:
\[D = \frac{1}{d} – \frac{2}{d}\]
\[D = – \frac{1}{d}\]
Окончательное получим такое решение задачи в общем виде:
\[d = – \frac{1}{D}\]
Подставим численные данные задачи в полученную формулу и посчитаем численный ответ (не забываем переводить величины в систему СИ):
\[d = \frac{-1}{{ – 5}} = 0,2\;м\]
Ответ: 0,2 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.5.59 На каком расстоянии от рассеивающей линзы с фокусным расстоянием 10 см находится
10.5.61 Светящаяся точка находится в фокусе рассеивающей линзы. На каком расстоянии от линзы
10.5.62 Середина стержня, имеющего длину 10 мм, находится на расстоянии 18 см от собирающей
Вы уверены, что рисунок верный?
Почему т.А совпадает с фокусом F ?
Да, конечно. Если Вы вычислите фокусное расстояние \(F\) через оптическую силу линзы \(D\), то получите 0,2 м. Такое же значение Вы получили для расстояния от линзы до предмета \(d\). Получается, что \(d=F\).