Решение: Дифракционная решетка, имеющая 100 штрихов на 1 мм, находится на расстоянии 1 м

Условие задачи:

Дифракционная решетка, имеющая 100 штрихов на 1 мм, находится на расстоянии 1 м от экрана и освещается белым светом. Найти ширину дифракционного спектра первого порядка на экране, если \(\lambda_{ф} = 0,4\) мкм, а \(\lambda_{кр} = 0,76\) мкм.

Задача №10.7.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(N=100\), \(l=1\) мм, \(L=1\) м, \(k=1\), \(\lambda_{ф}=0,4\) мкм, \(\lambda_{к}=0,76\) мкм, \(a-?\)

Решение задачи:

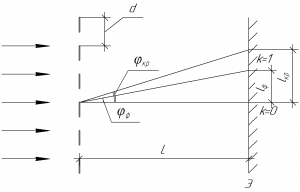Для начала вспомним формулу дифракционной решетки:

\[d\sin \varphi = k\lambda\;\;\;\;(1)\]

В этой формуле \(d\) — период решетки (также называют постоянной решетки), \(\varphi\) — угол дифракции, \(k\) — порядок максимума (в данной задаче \(k=1\)), \(\lambda\) — длина волны, падающей нормально на решетку.

Кстати, из формулы (1) прекрасно видно, что чем больше длина волны, тем больше угол дифракции, поэтому дифракционный максимум красного цвета находится выше дифракционного максимума фиолетового цвета (для максимумов одного порядка, разумеется). Поэтому искомую ширину дифракционного спектра первого порядка \(a\) будем искать по формуле:

\[a = {l_{кр}} — {l_ф}\;\;\;\;(2)\]

Запишем формулу (1) для крайних цветов видимого спектра излучения (т.е. для красного и фиолетового), естественно, свет каждой длины волны будет иметь свой собственный угол дифракции и свой дифракционный максимум:

\[\left\{ \begin{gathered}
d\sin {\varphi _{кр}} = k{\lambda _{кр}} \hfill \\
d\sin {\varphi _ф} = k{\lambda _ф} \hfill \\
\end{gathered} \right.\]

Если расписать синусы углов дифракции, учитывая их малость (то есть \(\sin \varphi \approx tg\varphi\)), то имеем:

\[\left\{ \begin{gathered}
d\frac{{{l_{кр}}}}{L} = k{\lambda _{кр}} \hfill \\
d\frac{{{l_ф}}}{L} = k{\lambda _ф} \hfill \\
\end{gathered} \right.\]

Тогда:

\[\left\{ \begin{gathered}
{l_{кр}} = \frac{{k{\lambda _{кр}}L}}{d} \hfill \\
{l_ф} = \frac{{k{\lambda _ф}L}}{d} \hfill \\
\end{gathered} \right.\]

В таком случае формула (2) примет вид:

\[a = \frac{{k{\lambda _{кр}}L}}{d} — \frac{{k{\lambda _ф}L}}{d}\]

\[a = \frac{{kL}}{d}\left( {{\lambda _{кр}} — {\lambda _ф}} \right)\]

Период (постоянную) решетки \(d\) можно определить, разделив некоторую длину решетки \(l\) на количество содержащихся на этой длине штрихов \(N\), то есть:

\[d = \frac{l}{N}\;\;\;\;(3)\]

Учитывая формулу (3), окончательно имеем:

\[a = \frac{{kLN}}{l}\left( {{\lambda _{кр}} — {\lambda _ф}} \right)\]

Задача решена в общем виде, подставим данные из условия в полученную формулу и посчитаем численный ответ:

\[a = \frac{{1 \cdot 1 \cdot 100}}{{{{10}^{ — 3}}}}\left( {0,76 \cdot {{10}^{ — 6}} — 0,4 \cdot {{10}^{ — 6}}} \right) = 0,036\;м = 3,6\;см\]