Посередине откачанной и запаянной с обоих сторон горизонтально

Условие задачи:

Посередине откачанной и запаянной с обоих сторон горизонтально расположенной трубки длиной 1 м находится столбик ртути длиной 20 см. Если трубку поставить вертикально, столбик ртути сместится на расстояние 10 см. До какого давления была откачана трубка?

Задача №4.3.37 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(L=1\) м, \(h=20\) см, \(\Delta l =10\) см, \(p_0-?\)

Решение задачи:

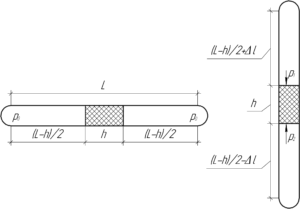Над двумя частями газа (смотри рисунок справа) будет производиться изотермический процесс (\(T=const\)). Когда трубка располагалась горизонтально, то обе части газа занимали объем трубки по длине \(\frac{{L – h}}{2}\). Когда же трубку поставят вертикально, то столбик ртути сместиться вниз, при этом верхняя часть газа займет объем по длине \(\frac{{L – h}}{2} + \Delta l\), а нижняя – \(\frac{{L – h}}{2} – \Delta l\).

Запишем закон Бойля-Мариотта для двух частей газа (объем сразу распишем как произведение длины на площадь сечения трубки) и закон Паскаля для случая вертикально расположенной трубки:

\[\left\{ \begin{gathered}
{p_0}S\frac{{L – h}}{2} = {p_1}S\left( {\frac{{L – h}}{2} + \Delta l} \right) \;\;\;\;(1) \hfill \\
{p_0}S\frac{{L – h}}{2} = {p_2}S\left( {\frac{{L – h}}{2} – \Delta l} \right) \;\;\;\;(2) \hfill \\
{p_1} + \rho gh = {p_2} \;\;\;\;(3) \hfill \\
\end{gathered} \right.\]

Из равенств (1) и (2) выразим \(p_1\) и \(p_2\) и подставим в (3), получим:

\[{p_0}\frac{{L – h}}{{L – h + 2\Delta l}} + \rho gh = {p_0}\frac{{L – h}}{{L – h – 2\Delta l}}\]

Остается только выразить искомое \(p_0\), сделаем это следующим образом:

\[{p_0}\frac{{L – h}}{{L – h – 2\Delta l}} – {p_0}\frac{{L – h}}{{L – h + 2\Delta l}} = \rho gh\]

Приведем слева под общий знаменатель:

\[\frac{{{p_0}\left( {L – h} \right)\left( {L – h + 2\Delta l} \right) – {p_0}\left( {L – h} \right)\left( {L – h – 2\Delta l} \right)}}{{\left( {L – h – 2\Delta l} \right)\left( {L – h + 2\Delta l} \right)}} = \rho gh\]

\[\frac{{4{p_0}\Delta l\left( {L – h} \right)}}{{{{\left( {L – h} \right)}^2} – 4\Delta {l^2}}} = \rho gh\]

В итоге получится следующая формула в общем виде:

\[{p_0} = \frac{{\rho gh\left( {{{\left( {L – h} \right)}^2} – 4\Delta {l^2}} \right)}}{{4\Delta l\left( {L – h} \right)}}\]

Подставив в нее численные данные обязательно в системе СИ, будет иметь и ответ в системе СИ. Поскольку требуется найти начальное давление, то по результатам расчета оно будет в Па.

\[{p_0} = \frac{{13600 \cdot 10 \cdot 0,2\left( {{{\left( {1 – 0,2} \right)}^2} – 4 \cdot {{0,1}^2}} \right)}}{{4 \cdot 0,1\left( {1 – 0,2} \right)}} = 51000 \; Па = 51 \; кПа\]

Ответ: 51 кПа.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

4.3.36 В стеклянной трубке находится столбик ртути длиной 10 см. Когда
4.3.38 Открытую с обеих сторон стеклянную трубку длиной 60 см
4.3.39 В трубке длиной 1,73 м, заполненной газом, находится столбик ртути